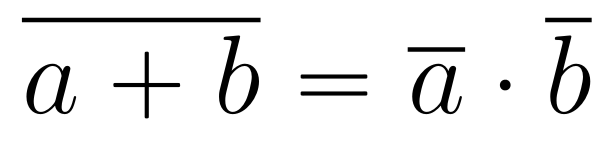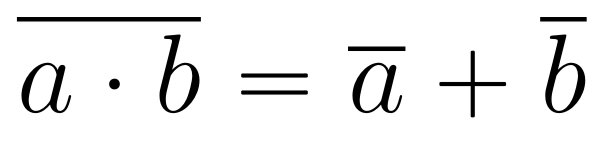05 Cours Logique booléenne
Logique⚓︎
La logique est une forme d’opération de la pensée qui nous permet de raisonner.
On s'intéresse par exemple à la phrase :« Ce soir, j'irai me promener s’il fait beau et si j’ai fini mon travail. »
Nous tenterons de la ramener à des choix simples où les affirmations sont soit vraies soit fausses, les réponses aux questions sont oui ou non, il n’y a pas de valeurs intermédiaires. La promenade est liée à deux conditions : la météo et le travail qui reste à faire. Les différentes situations sont représentées dans ce qu’on appelle une table de vérité :
| Il fera beau | Mon travail sera achevé | J’irai me promener |
|---|---|---|
| Non | Non | Non |
| Non | Oui | Non |
| Oui | Non | Non |
| Oui | Oui | Oui |
Essayer avec la proposition suivante : « l’accusé sera disculpé si l’enquête révèle qu’il s’agit d’un suicide ou s’il peut faire la preuve qu’il était ailleurs au moment des faits. » Dans ce cas, une seule des deux conditions suffit pour disculper l’accusé.
Histoire⚓︎
Bon nombre de chercheurs ont tenté de trouver une manière infaillible de raisonner. George Boole traduisit les relations logiques en équations ce qui donna l’ algèbre de Boole. Il définit ainsi les règles qui permettent de faire des raisonnements valides pour autant que les « variables logiques » ne puissent avoir que deux valeurs possibles : Oui ou Non, Vrai ou faux, 1 ou 0. Les variables sont des « variables binaires ».
Shannon (1916-2001), l’inventeur du mot « bit », démontra que l’algèbre de Boole était applicable aux circuits électriques. Cela permit à cette époque d’automatiser les centraux téléphoniques. Aujourd’hui, les transistors , de l’anglais transfer resistor (résistance de transfert), que l’on trouve dans les circuits, se comportent comme des interrupteurs. N’importe quel ordinateur ou smartphone en contient plusieurs milliards sur une simple puce de silicium de la taille d’un ongle.
Définitions⚓︎
-
Un booléen, en logique et en programmation informatique, est un type de variable à deux états. Les variables de ce type sont ainsi soit à l’état vrai soit à l’état faux (en anglais true et false). On convient de lire 0 comme « faux » et 1 comme « vrai ».
-
On appelle fonction logique une fonction qui associe un booléen à un ou plusieurs booléen(s).
Opérateurs booléens de base⚓︎
Les opérations logiques sont, en informatique, aussi courantes, si ce n’est plus, que les opérations arithmétiques. La logique combinatoire, tout comme l’arithmétique, repose sur quelques opérations élémentaires.
- En arithmétique, ces opérations sont l’addition, la soustraction, la multiplication et la division (+, -, *, /). Il est possible à partir de là d’imaginer toutes les autres opérations telles que les exposants, les racines, les logarithmes, etc.
- En logique, les opérations fondamentales sont le ET, le OU et le NON.
La manière la plus simple de comprendre les opérateurs booléens est de se les représenter par des schémas électriques. Voici, par exemple, l’opérateur OUI :

Cet opérateur utilise simplement un interrupteur normalement ouvert. Le voyant ne s’allume que si l’interrupteur est actionné.
Si nous appelons \(s\) la sortie et \(a\) l’entrée, le fonctionnement de ce circuit s’exprime par l’équation logique \(s=a\). Il n’y a que deux cas possibles. Ils sont représentés dans cette table de vérité.
| \(a\) | \(s\) |
|---|---|
| 0 | 0 |
| 1 | 1 |
Une table de vérité a pour le rôle de montrer la correspondance entre la sortie et toutes les combinaisons de valeurs que peuvent prendre la ou les entrées.
L’opérateur NON⚓︎
Symbole électronique (on parle de porte logique NON)⚓︎
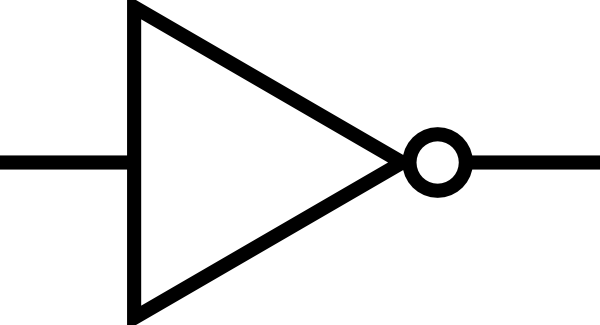
Circuit électrique⚓︎
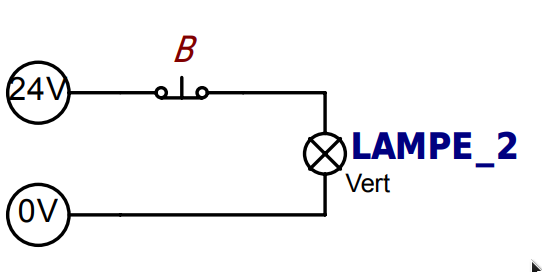
Pour obtenir cette fonction, il suffit de brancher un interrupteur normalement fermé. Le voyant s’allume tant que l’interrupteur n’est pas actionné.
Table de vérité⚓︎
La fonction non transforme faux en vrai et vrai en faux : le booléen \(non(a)\) est donc égal à 1 si et seulement si \(a\) n’est pas égal à 1.
| \(a\) | \(s\) |
|---|---|
| 0 | 1 |
| 1 | 0 |
Notation et équation logique⚓︎
\(s=\overline{a}\)
Lire « s = Non a »
Propriétes⚓︎
- \(\overline{\overline{a}}=a\)
- \(\overline{\overline{\overline{a}}}=\overline{a}\)
L’opérateur ET⚓︎
Symbole électronique (on parle de porte logique ET)⚓︎

Circuit électrique⚓︎
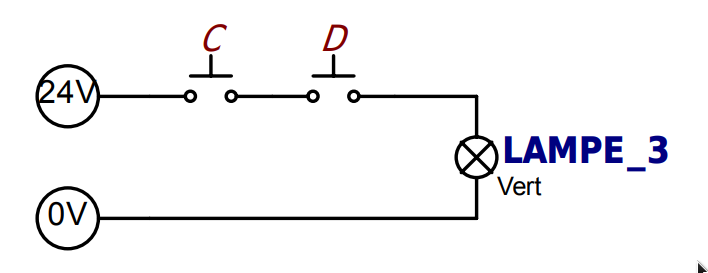
Pour obtenir cette fonction, il suffit de brancher deux interrupteurs normalement ouverts en série. Pour que le courant puisse traverser le voyant et l’allume, il faut actionner simultanément les deux interrupteurs.
Table de vérité⚓︎
Le booléen a et b est égal à 1 si et seulement si a est égal à 1 et b est égal à 1.
Si nous notons \(s\) la sortie et \(a\) et \(b\) les deux entrées, nous obtenons ainsi :
| \(a\) | \(b\) | \(s\) |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
Notation et équation logique⚓︎
L’opérateur ET est représenté dans l’équation logique par un point. Ce signe convient parfaitement puisque la fonction ET donne le même résultat qu’une multiplication.
\(s=a \cdot b\)
On le note également :
\(s=a \land b\)
Propriétés du ET⚓︎
- \(a \cdot 1 = a\quad\) (élément neutre)
- \(a \cdot 0 = 0\quad\) (variable absorbée)
- \(a \cdot a = a\quad\) (idempotence)
- \(a \cdot \overline{a} = 0\)
- \(a \cdot b = b \cdot a\quad\) (commutativité)
- \(a \cdot b \cdot c = ( a \cdot b ) \cdot c = a \cdot ( b \cdot c )\quad\) (associativité)
L’opérateur OU⚓︎
Symbole électronique (on parle de porte logique OU)⚓︎
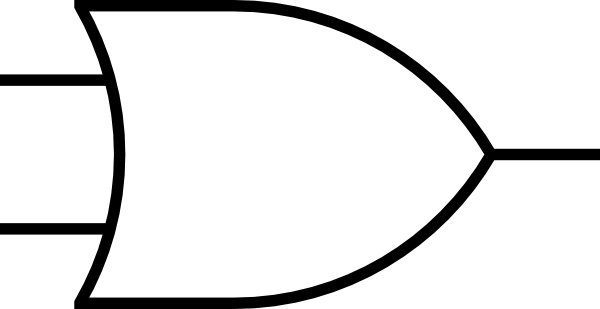
Circuit électrique⚓︎
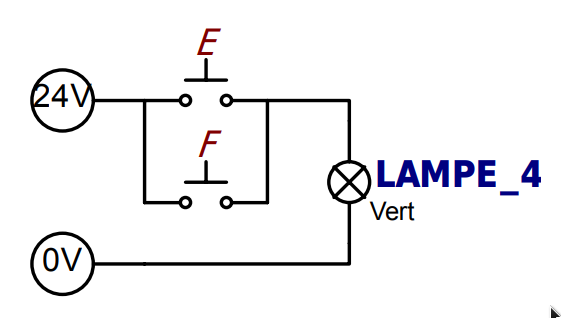
Pour obtenir cette fonction, il suffit de brancher deux interrupteurs normalement ouverts en parallèle. Le voyant s’allume dès que l’un des interrupteurs est actionné.
Table de vérité⚓︎
Le booléen a ou b est égal à 1 si et seulement si au moins a ou b est égal à 1.
| \(a\) | \(b\) | \(s\) |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 1 |
On remarquera que, quand \(a\) et \(b\) sont tous les deux égaux à \(1\), a ou b est égal à \(1\). Ce ou est donc inclusif ; c’est le ou qui apparaît dans la phrase « Je viendrais qu’il pleuve ou qu’il neige » et non le ou exclusif qui apparaît dans la phrase « Tu dois choisir : aller à la mer ou aller à la montagne ». Pour le distinguer du précédent, ce ou exclusif sera noté oux (en anglais xor).
Notation et équation logique⚓︎
L’opérateur OU est représenté par :
\(s=a+b\)
ou par :
\(s=a \lor b\)
Propriétés du OU⚓︎
- \(a + 1 = 1\quad\) (variable absorbée)
- \(a + 0 = a\quad\) (élément neutre)
- \(a + a = a\quad\) (idempotence)
- \(a + \overline{a} = 1\)
- \(a + b = b + a\quad\) (commutativité)
- \(a + b + c = ( a + b ) + c = a + ( b + c )\quad\) (associativité)
Propriétés des opérations booléennes entre elles⚓︎
Distributivité⚓︎
- \(a \cdot ( b + c ) = a \cdot b + a \cdot c\)
- \(( a + b ) \cdot ( c + d ) = a \cdot c + a \cdot d + b \cdot c + b \cdot d\)
- \(a + ( b \cdot c ) = ( a + b ) \cdot ( a + c )\)
Théorème de De Morgan⚓︎
Autrement dit, la négation d'un ET est un OU ; et la négation d'un OU est un ET :
la phrase "j'ai un chien ET un chat" est fausse si "je n'ai pas de chien OU je n'ai pas de chat (ou les deux, inutile de le préciser)".
Combinaisons de fonctions logiques⚓︎
Les trois fonctions de base que nous venons de voir se combinent de multiples façons. À chaque schéma imaginable correspond une équation logique. La correspondance entre un schéma et une fonction logique est systématique :
- des contacts en parallèle correspondent à la fonction OU ;
- des contacts en série correspondent à la fonction ET ;
- un contact normalement fermé représente la fonction NON.
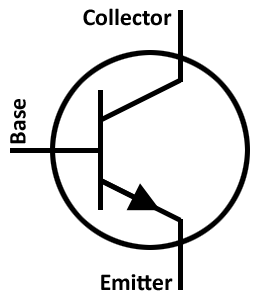
Dans un processeur, ce sont les transistors qui jouent le rôle des interrupteurs des schémas ci-dessus, à la différence que ceux-ci sont pilotés mécaniquement alors que les transistors sont actionnés électriquement.
Le transistor est une des briques essentielles de tout circuit électronique en général et d’un microprocesseur en particulier. Un transistor comporte 3 broches : la base, le collecteur et l’émetteur. Le collecteur reçoit le courant qui est commandé par la base et est transmit (ou pas) à l’émetteur.
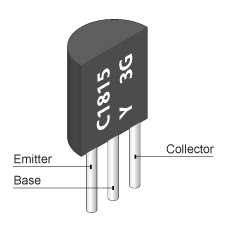
On peut résumer son comportement à celui d’un interrupteur. Si on alimente la base avec une tension suffisante (tension de seuil), un courant passe entre le collecteur et l’émetteur : le transistor est alors en régime saturé et se comporte comme un interrupteur fermé. Si la tension appliquée à la base est en dessous d’un certain seuil, il ne passe pas de courant entre le collecteur et l’émetteur : c’est le régime bloqué où le transistor se comporte comme un interrupteur ouvert. Entre ces deux états, le transistor connait un régime linéaire pendant lequel la tension passe de la tension d’alimentation à une tension nulle.