05 Exos Logique booléenne Correction
Exercice 1 - Fonctions NAND, NOR, XOR et XNOR⚓︎
Écrire les tables de vérité de chacune des fonctions suivantes.
- AND : ET ;
| \(a\) | \(b\) | \(a\) AND \(b\) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
- NAND : NON ET \(~~~~~~\)(Not AND) ;
| \(a\) | \(b\) | \(a\) AND \(b\) | \(a\) NAND \(b\) |
|---|---|---|---|
| 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
- OR : OU ;
| \(a\) | \(b\) | \(a\) OR \(b\) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
- NOR : NON OU \(~~~~~~\)(Not OR) ;
| \(a\) | \(b\) | \(a\) OR \(b\) | \(a\) NOR \(b\) |
|---|---|---|---|
| 0 | 0 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 |
- XOR : OU Exclusif \(~~~~~~\)(Exclusive OR) ;
| \(a\) | \(b\) | \(a\) XOR \(b\) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
- XNOR : NON OU Exclusif \(~~~~~~\)(Exclusive NOR).
| \(a\) | \(b\) | \(a\) NXOR \(b\) |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Exercice 2⚓︎
Construire la table de vérité de l’expression non (non(x) ou non(y)).
On prendra une colonne pour \(x\), une pour \(y\), une pour non(x), une pour non(y), une pour (non(x) ou non(y)) et une dernière pour l’expression complète.
Quelle fonction reconnaît-on ?
En déduire que toutes les fonctions booléennes peuvent s’exprimer à l’aide de deux fonctions, que l’on précisera.
| \(x\) | \(y\) | non(x) | non(y) | non(x) ou non(y) | non (non(x) ou non(y)) |
|---|---|---|---|---|---|
| 0 | 0 | 1 | 1 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 | 1 |
On reconnaît la fonction ET.
Donc x ET y = non(non(x) OU non(y))
Toutes les fonctions peuvent s'exprimer en fonction de ET, OU et NON ; donc en exprimant ET grâce à NON et OU, toutes les fonctions booléennes peuvent être exprimées uniquement en fonction de NON et OU.
Exercice 3⚓︎
Montrer (à l’aide d’une table de vérité similaire à celle de l’exercice précédent) que x ou y = non (non(x) et non(y)).
En déduire que toutes les fonctions booléennes peuvent s’exprimer avec les fonctions non et et.
| \(x\) | \(y\) | non(x) | non(y) | non(x) et non(y) | non (non(x) et non(y)) |
|---|---|---|---|---|---|
| 0 | 0 | 1 | 1 | 1 | 0 |
| 0 | 1 | 1 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 0 | 1 |
On reconnaît la fonction OU.
Donc x OU y = non(non(x) ET non(y))
Conclusion : comme toutes les fonctions booléennes s'expriment avec ou, non, et et, on peut remplacer les ou par x OU y = non(non(x) ET non(y)), et la fonction booléenne sera ainsi exprimée uniquement avec des non et des et.
Exercice 4⚓︎
Montrer que non(x ou y) = non(x) et non(y) puis que non(x et y) = non(x) ou non(y).
| x | y | x ou y | non(x ou y) |
|---|---|---|---|
| 0 | 0 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 |
| x | y | non(x) | non(y) | non(x) et non(y) |
|---|---|---|---|---|
| 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 |
Donc non(x ou y) = non(x) et non(y)
Et avec x' = non(x) et y' = non(y), on obtient :
non(x et y) = non(non(x') et non(y')) = non(non(x' ou y')) = x' ou y' = non(x) ou non(y)
Exercice 5⚓︎
Compléter la table de vérité de la porte logique suivante puis donner son expression booléenne.
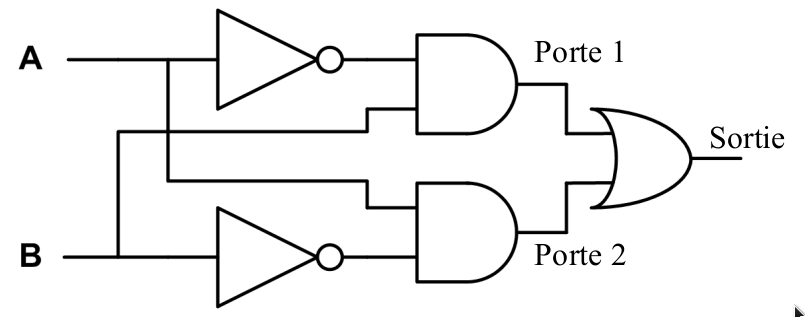
porte 1 = non(A) ET B
porte 2 = A ET non(B)
sortie = porte 1 OU porte 2
| \(A\) | \(B\) | \(\overline{A}\) | \(\overline{B}\) | Porte 1 | Porte 2 | Sortie |
|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 |
Exercice 6 - Multiplexeur⚓︎
On définit la fonction multiplexeur, notée mux, de \(B^3\) dans \(B\) par :
\(mux(A,y,z) = (non(A)\text{ } et \text{ } y)\text{ } ou\text{ } (A\text{ } et\text{ } z)\).
Compléter la table suivante.
| A | y | z | non(A) | non(A) et y | A et z | mux(A, y , z) |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 | 1 | 1 |
On remarque que :
- si \(A = 0\), alors \(mux(A,y,z) = y\)
- si \(A = 1\), alors \(mux(A,y,z) = z\)
En fait, lorsqu'on a deux entrées \(x\) et \(y\), ou (ce qui revient au même) une entrée sur 2 bits, le multiplexeur permet de sélectionner la valeur de l'une de ces entrées en indiquant sont numéro dans le bit \(A\).
Il existe des multiplexeurs avec davantage d'entrées : par exemple, on aura 8 entrées e0, e1, e2, e3, e4, e5, e6, e7, et deux autres entrées A0 et A1, qui permettent de coder sur 2 bits le numéros (entre 0 et 7) de la valeur d'entrée que l'on souhaite sélectionner...
Exercice 7⚓︎
La fonction de Sheffer exprime l’incompatibilité de deux valeurs booléennes. Elle est définie par S(x, y) = non(x et y).
- Montrer que S(x,x) = non(x).
Par une table de vérité :
| \(x\) | \(x\) et \(x\) | \(S(x, x)\) | non(\(x\)) |
|---|---|---|---|
| 0 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
donc S(x,x) = non(x)
Ou alors par simplification de formule booléenne :
S(x,x) = non(x et x) = non(x)
- Puis montrer que S(S(x,x),S(y,y)) = x ou y.
Par une table de vérité :
| \(x\) | \(y\) | \(S(x, x)\) | \(S(y,y)\) | \(S(S(x,x),S(y,y))\) | \(x\) ou \(y\) |
|---|---|---|---|---|---|
| 0 | 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 | 0 |
donc S(S(x,x),S(y,y)) = x ou y
Ou alors par simplification de formule booléenne :
S(S(x,x),S(y,y)) = S(non(x), non(y)) = non(non(x) et non(y)) = non(non(x)) ou non(non(y)) = x ou y
- En déduire que toutes les fonctions booléennes peuvent s’exprimer avec la fonction de Sheffer uniquement. Toute fonction booléenne peut donc être exprimée à l’aide de la seule fonction NAND (non-et). Donc, tout circuit logique pourrait être constitué de seules portes NAND.
Exercice 8⚓︎
Med est content si Bob et Jon sont tous les deux là, mais sans Rut, ou si Rut est là soit avec Bob, soit avec Jon. Construire une table avec en entrée la présence de Rut, Bob et Jon et en sortie le booléen qui vaut 1 si Med est content. Exprimer le choix de Med par une phrase plus simple.
0 = absent ; 1 = présent
| Rut | Bob | Jon | Med |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
Med est content si exactement 2 personnes sur les 3 sont présentes parmi Bob, Jon et Rut.
Exercice 9 - Simplification d’expressions logiques⚓︎
Simplifier les équations logiques ci-dessous en utilisant l’algèbre de Boole.
- \(A=a+a\cdot b\)
\(A=a+a\cdot b = a \cdot (1 + b) = a \cdot 1 = a\) - \(B=a\cdot(a+b)\)
\(B=a\cdot(a+b) = a \cdot a + a \cdot b = a + a \cdot b = A = a\) - \(C=a+\overline{a}\cdot b\)
\(C=a+\overline{a}\cdot b = A + \overline{a}\cdot b = a+a\cdot b + \overline{a}\cdot b = a + (a + \overline{a})\cdot b = a + 1\cdot b = a + b\) - \(D=(a+b)\cdot(a+\overline{b})\)
\(D=(a+b)\cdot(a+\overline{b}) = a \cdot a + a \cdot \overline{b} + a \cdot b + b \cdot \overline{b} = a + a \cdot (\overline{b} + b) + 0 = a + a \cdot 1 = a + a = a\) - \(E=(a+b)\cdot(a+c)\)
\(E=(a+b)\cdot(a+c) = a \cdot a + a \cdot c + a \cdot b + b \cdot c = a + a \cdot (c + b) + b \cdot c = a + b \cdot c~~~\) (voir \(A\)) - \(F=(a+b)\cdot(\overline{a}+c)\)
\(F=(a+b)\cdot(\overline{a}+c) = a \cdot \overline{a} + a \cdot c + \overline{a} \cdot b + b \cdot c = (a+b) \cdot c + \overline{a} \cdot b\)
Mais on peut faire mieux, en utilisant, par exemple, l'égalité du \(C\).
\(F=(a+b)\cdot(\overline{a}+c) = (a+\overline{a}\cdot b)\cdot(\overline{a}+c)\)
\(F = a \cdot \overline{a} + a \cdot c + \overline{a} \cdot \overline{a} \cdot b + \overline{a} \cdot b \cdot c = 0 + a \cdot c + \overline{a} \cdot b \cdot (1 + c) = a \cdot c + \overline{a} \cdot b\) - \(G=(\overline{a}+\overline{b}) \cdot (\overline{a}+b) \cdot (a+\overline{b})\)
\(G=(\overline{a} \cdot \overline{a} + \overline{b} \cdot \overline{a} + \overline{a} \cdot b + \overline{b} \cdot b) \cdot (a+\overline{b})\)
\(G = (\overline{a} + \overline{a} \cdot (\overline{b} + b) + 0) \cdot (a + \overline{b})\)
\(G = \overline{a} \cdot (a+\overline{b}) = \overline{a} \cdot a + \overline{a} \cdot \overline{b} = 0 + \overline{a} \cdot \overline{b} = \overline{a} \cdot \overline{b}\) - \(H=(a \cdot b)+(\overline{a} \cdot b)+(a \cdot \overline{b})\)
\(H=a \cdot (b + \overline{b})+(\overline{a} \cdot b)\)
\(H=a \cdot 1 +(\overline{a} \cdot b)\)
\(H=a + (\overline{a} \cdot b)\)
\(H=C = a + b\)
Exercice 10⚓︎
Sur la planète CSI vivent les Profs (qui disent toujours la vérité) et les Élèves (qui mentent toujours). Vous croisez deux personnes A et B sur cette planète. A affirme : « Au moins l’un de nous deux est un élève ». Dire ce que sont A et B.
On peut étudier les différentes configurations possibles pour A et B.
Et on considère la phrase C : « Au moins l’un de nous deux est un élève ».
| A | B | C | Cohérence avec A |
|---|---|---|---|
| Prof | Prof | F | Non |
| Prof | Élève | V | OK |
| Élève | Prof | V | Non |
| Élève | Élève | V | Non |
La seule possibilité est donc que A soit un Prof et B soit un Élève.
Exercice 11 : pour s'amuser un peu⚓︎
Trois hommes sont l’un derrière l’autre.
Chacun porte un chapeau sur la tête tiré au hasard parmi 3 chapeaux noirs et 2 chapeaux blancs.
Ils ne savent pas eux-même quel chapeau ils ont sur la tête. L’homme C voit les deux autres, l’homme B ne voit que l’homme A, et l’homme A ne voit personne.
- On demande à l’homme C s’il connait la couleur de son chapeau. Celui-ci répond que non.
- On pose la même question à l’homme B qui lui non plus dit ne pas savoir la couleur de son chapeau.
- Même question pour l’homme A qui lui sait quelle est la couleur de son chapeau.
Quelle est la couleur du chapeau de A ?
| A | B | C | C connait sa couleur |
|---|---|---|---|
| noir | noir | noir | Non |
| noir | noir | blanc | Non |
| noir | blanc | noir | Non |
| noir | blanc | blanc | Non |
| blanc | noir | noir | Non |
| blanc | noir | blanc | Non |
| blanc | blanc | noir | Oui |
Lorsque C répond qu'il ne connaît pas sa couleur, les deux autres peuvent en déduire qu'on n'est pas dans la configuration A blanc, B blanc, C noir.
| A | B | C | C connait sa couleur | B connaît sa couleur |
|---|---|---|---|---|
| noir | noir | noir | Non | Non |
| noir | noir | blanc | Non | Non |
| noir | blanc | noir | Non | Non |
| noir | blanc | blanc | Non | Non |
| blanc | noir | noir | Non | Oui |
| blanc | noir | blanc | Non | Oui |
Lorsque B répond qu'il ne connaît pas sa couleur, les deux autres peuvent en déduire qu'on n'est pas dans la configuration A blanc, B noir, C noir ou blanc.
A sait alors que sa couleur de chapeau est noire.
On n'a pas davantage d'information sur les couleurs de B et C.