05bis Exos TP Circuits Logiques

Objectif

Concevoir et tester des circuits logiques simples et les expressions booléennes associées à l’aide d’un logiciel de simulation.

Tout particulièrement, concevoir le circuit électrique permettant d'effectuer l'addition de deux nombres écrits en binaire.

Consignes

• Vous devez répondre aux questions demandées sur votre feuille.
• Vous devez m’envoyer par mail un fichier compressé dont le nom sera prenom_TP_Logisim.zip. Ce fichier compressé contiendra les fichiers sources des circuits réalisés avec le logiciel Logisim (fichiers avec l’extension circ).

Prise en main du logiciel Logisim

Le logiciel Logisim est un simulateur de circuits logiques. C’est un logiciel libre et gratuit. Il est écrit en Java avec la bibliothèque graphique Swing.

Voici une petite vidéo vous permettant de prendre en main de logiciel :

Voici un premier circuit logique composé de deux portes not, de deux portes and et d’une porte or :

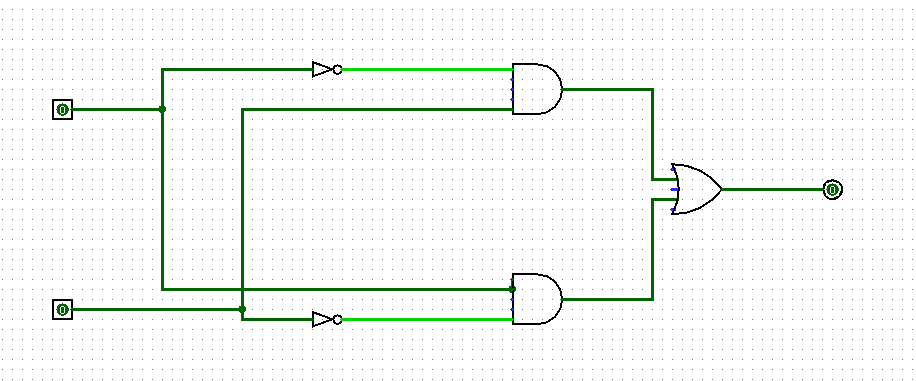
1. Construire ce circuit logique avec le logiciel Logisim et enregistrer le fichier sous le nom « circuit1 ».
2. Établir sur votre feuille la table de vérité de ce circuit logique.
3. Ce circuit implémente une porte logique que vous devez connaitre. Quelle est cette porte logique ?
4. À partir de la représentation graphique de ce circuit logique, établir son expression.

Additionneur

Demi additionneur

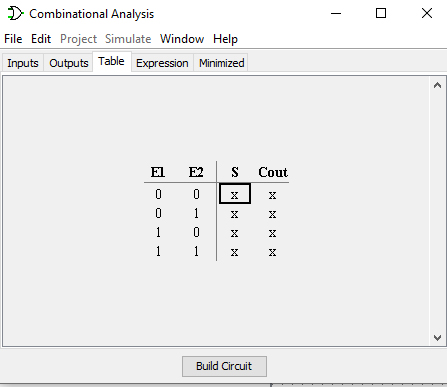
Table de vérité du demi additionneur

Écrire la table de vérité d’un additionneur de deux bits avec en entrées les deux bits à addtionner (E1 et E2) et en sorties le bit de sortie (S) et la retenue éventuelle (Cout).

Circuit logique du demi additionneur

Implémenter la table de vérité dans le logiciel Logisim dans la partie Window/Combinational Analysis du demi additionneur et demander au logiciel de construire automatiquement le circuit logique correspondant.

Voici une vidéo qui explique les manipulations à effectuer pour construire automatiquement un circuit logique à partir de sa table de vérité.

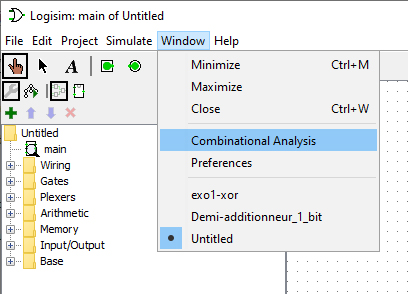
Équation du demi additionneur

Donner les expressions (Sortie et Retenue) du demi-additionneur à l’aide des fonctions logiques not, or et and.

Enregistrer le fichier sous le nom Demi_additionneur_1_bit.

Additionneur complet

Un additionneur complet nécessite une entrée supplémentaire : une retenue. L’intérêt de celle-ci est de permettre le chaînage des circuits.

Table de vérité de l’additionneur complet

Écrire la table de vérité d’un additionneur complet avec en entrées les deux bits à additionner (E1 et E2), une retenue (Cin) et en sorties le bit de sortie et la retenue (Cout).

Circuit logique de l’additionneur complet

Implémenter la table de vérité dans le logiciel Logisim de l’additionneur complet et demander au logiciel de construire automatiquement le circuit logique correspondant.

Equation de l’additionneur complet

Donner les équations (Sortie et Retenue) de l’additionneur complet à l’aide des fonctions logiques not, or et and.

Enregistrer le fichier sous le nom Additionneur_complet_1_bit.

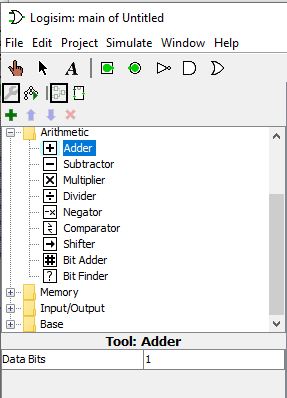
Additionneur complet avec plusieurs bits

Le composant Adder dans la catégorie Arithmetic avec Data bits = 1 représente l’additionneur complet 1 bit dont nous venons de construire le circuit logique.

Additionneur complet sur 2 bits

En enchainant deux additionneurs complets 1 bit, construire avec Logisim le circuit logique d’un additionneur complet 2 bits.

Tester votre circuit logique en additionnant des nombres binaires sur 2 bits.

Enregistrer le fichier sous le nom Additionneur_complet_2_bits.

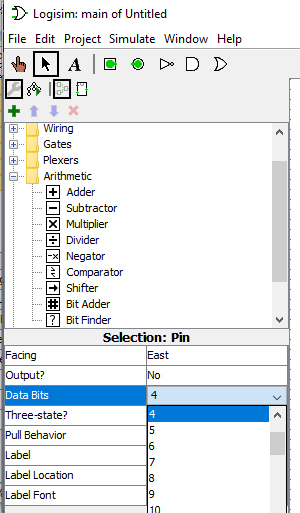
Additionneur complet sur 4 bits

En utilisant le composant Adder avec Data bits = 4 construire le circuit logique permettant de faire l’addition binaire de deux nombres sur 4 bits.

Tester cet additionneur 4 bits.

Enregistrer le fichier sous le nom Additionneur_complet_4_bits.

Travail à rendre

Créer un fichier compressant au format zip nommé prenom_TP_Logisim.zip contenant les fichiers suivants :

• circuit1.circ
• Demi_additionneur_1_bit.circ
• Additionneur_complet_1_bit.circ
• Additionneur_complet_2_bits.circ
• Additionneur_complet_4_bits.circ

M’envoyer par mail ce fichier compressé.

Pour ceux qui ont terminé

Les multiplexeurs

Dans l'exercice 6 de la fiche "logique booléenne", on vous a présenté le multiplexeur.

On définit la fonction multiplexeur, notée mux, de \(B^3\) dans \(B\) par :
\(mux(A,y,z) = (non(A)\text{ } et \text{ } y)\text{ } ou\text{ } (A\text{ } et\text{ } z)\).
Compléter la table suivante.

A	y	z	non(A)	non(A) et y	A et z	mux(A, y , z)
0	0	0	1	0	0	0
0	0	1	1	0	0	0
0	1	0	1	1	0	1
0	1	1	1	1	0	1
1	0	0	0	0	0	0
1	0	1	0	0	1	1
1	1	0	0	0	0	0
1	1	1	0	0	1	1

Un multiplexeur est un circuit permettant de concentrer sur le même circuit plusieur entrées de données, et de sélectionner laquelle sera transmise en sortie en fonction de la valeur d'une entrée de commande.

Dans notre exemple,
si A = 0, alors la sortie vaut y ;
si A = 1, alors la sortie vaut z.

A est le bit de commande, il a permis de choisir de transmettre la donnée \(y\) (numérotée 0) ou la donnée \(z\) (numérotée 1).

On peut ainsi remarquer que, s'il y a 4 entrées de données \(e0\), \(e1\), \(e2\), \(e3\), nous aurons besoin de 2 bits de commande afin de sélectionner quelle données d'entrée sera transmise en sortie.
Par exemple, pour transmettre \(e2\), on saisira \(10\) en commande.

1. De combien de bits de commande aura-t-on besoin pour un multiplexeur à 8 entrées de données ?
2. Réalisez, sur le logiciel Logisim, le circuit du multiplexeur qui prend 2 bits de données en entrée et sort 1 bit.
3. Ecrire la table de vérité d'un multiplexeur qui prend 4 bits de données en entrée et sort 1 bit.
4. Réalisez, sur le logiciel Logisim, le circuit de ce multiplexeur (qui prend 4 bits de données en entrée et sort 1 bit).

Nota Bene : le logiciel Logisim contient des éléments multiplexeur, mais comme pour l'addition, dans un premier temps, le but n'est pas d'utiliser l'obejt tout fait...

La soustraction

Nous avons travaillé sur l'additionneur 1 bit, puis 2 bits, ...
Serez-vous capables de faire une soustraction ?
Première remarque : nous allons travailler avec des nombres relatifs (codé en binaire par le complément à 2)...
Remarquons maintenant que \(A - B = A + (-B)\).
On pourrait donc réutiliser l'additionneur si on pouvait récupérer \(-B\).
Le cours sur le binaire nous indique comment obtenir \(-B\) à partir de \(B\) avec le complément à deux.
1. Ecrire la table de vérité du passage à l'opposé pour un nombre codé sur 2 bits.
2. Ecrire la table de vérité du passage à l'opposé pour un nombre codé sur 4 bits.
3. Réaliser les circuits correspondants sur Logisim.
4. En enchaînant avec un additionneur, réaliseur un soustracteur...