20 Cours Complexité
Questions fondamentales⚓︎
Les trois questions fondamentales à se poser à propos de tout algorithme sont les suivantes :
- donne-t-il un résultat ou ne s’arrête-t-il jamais ? (Notion de terminaison) ;
- donne-t-il le résultat attendu ou calcule-t-il autre chose ? (Notion de correction) ;
- donne-t-il le résultat en un temps raisonnable ou faut-il attendre très longtemps ? (Notion de complexité).
Complexité⚓︎
Principe⚓︎
Dans ce chapitre, nous nous contenterons d’exposer le principe du coût en temps (ou en nombre d’opérations) et non pas en espace mémoire. Essayons de répondre à la question suivante : combien de temps un algorithme implémenté par un programme prend à s’exécuter ?
Le temps d’exécution d’un programme dépend de la taille des données fournies en entrée. En effet, on peut facilement concevoir que le programme ci-dessus n’a pas le même temps d’exécution selon que l’on ait, en paramètre, une liste de vingt mots ou l’ensemble du dictionnaire de la langue française.
Les ordinateurs n’ayant pas tous la même vitesse d’exécution (fréquence du processeur, vitesse de la RAM, débit du disque dur, etc.) il convient d’évaluer le coût en temps d’un algorithme indépendamment de l’architecture de l’ordinateur utilisé. Il convient donc de raisonner en terme de nombre d’opérations qu’un programme doit effectuer lors de son exécution : par convention, chaque opération simple (opération arithmétique, comparaison, affectation, appel de fonction, instruction de contrôle if, etc.) correspond à exactement une étape de calcul. On parle de temps constant.
Pour essayer d’estimer le temps que prend un programme à s’exécuter, on peut se servir du « meilleur des cas » (temps minimal pour toutes les entrées possibles), du « cas moyen » (temps moyen pour toutes les entrées possibles) ou du « pire des cas » (temps maximal pour toutes les entrées possibles). Nous nous intéresserons exclusivement au temps d’exécution correspondant au « pire des cas », c’est à dire au temps d’exécution maximal. Imaginons, par exemple, que le programme ci-dessus se termine dès que l’élément est atteint ; le temps d’exécution au pire des cas correspondrait alors au cas où l’élément recherché est en dernière position de la liste. Le temps d’exécution au pire des cas est donc le temps maximal que met un algorithme à se terminer quand il reçoit des données d’une certaine taille.
Classes de complexité⚓︎
Il est possible de catégoriser les algorithmes par classes de complexité. Des algorithmes appartenant à une même classe seront alors considérés comme étant de complexité équivalente et comme ayant la même efficacité (ce qui est vrai pour des données de grandes tailles). Voici les complexités de référence rangées par ordre croissant de temps d’exécution :
- \(1\) : complexité constante – accès à une valeur d’une liste
- \(\log(n)\) : complexité logarithmique – recherche dichotomique dans une liste triée
- \(n\) : complexité linéaire – parcours d’une liste
- \(n\log(n)\) : complexité quasi-linéaire – tri fusion, le tri
sort()de python - \(n^2\) : complexité quadratique – parcours d’une liste de liste (tableau \(n \times n\))
- \(2^n\) : complexité exponentielle – calcul d’un terme de la suite de Fibonacci
- \(n!\) : complexité factorielle – problème du voyageur de commerce
Qu'est-ce-que la factorielle ?
\(n! = 1 \times 2 \times .. \times n\)
La factorielle croît très vite :
1! = 1
2! = 1 × 2 = 2
3! = 1 × 2 × 3 = 6
4! = 1 × 2 × 3 × 4 = 24
10! = 1 × 2 × 3 × 4 × 5 × 6 × 7 × 8 × 9 × 10 = 3 628 800
Pour les grandes valeurs, \(n!\) est de l'ordre de \(n^n\).
| Big-O | 10 éléments en entrée | 100 éléments en entrée |
|---|---|---|
| \(\mathcal{O}(1)\) | 1 | 1 |
| \(\mathcal{O}(\log(n)\) | 3 | 7 |
| \(\mathcal{O}(n)\) | 10 | 100 |
| \(\mathcal{O}(n\log(n))\) | 30 | 700 |
| \(\mathcal{O}(n^2)\) | 100 | \(10000 = 10^{4}\) |
| \(\mathcal{O}(2^n)\) | 1024 | \(2^{100} \approx 10^{30}\) |
| \(\mathcal{O}(n!)\) | 3628800 | \(100! \approx 10^{158}\) |
Le graphique ci-dessous donne une idée de la différence entre les classes.
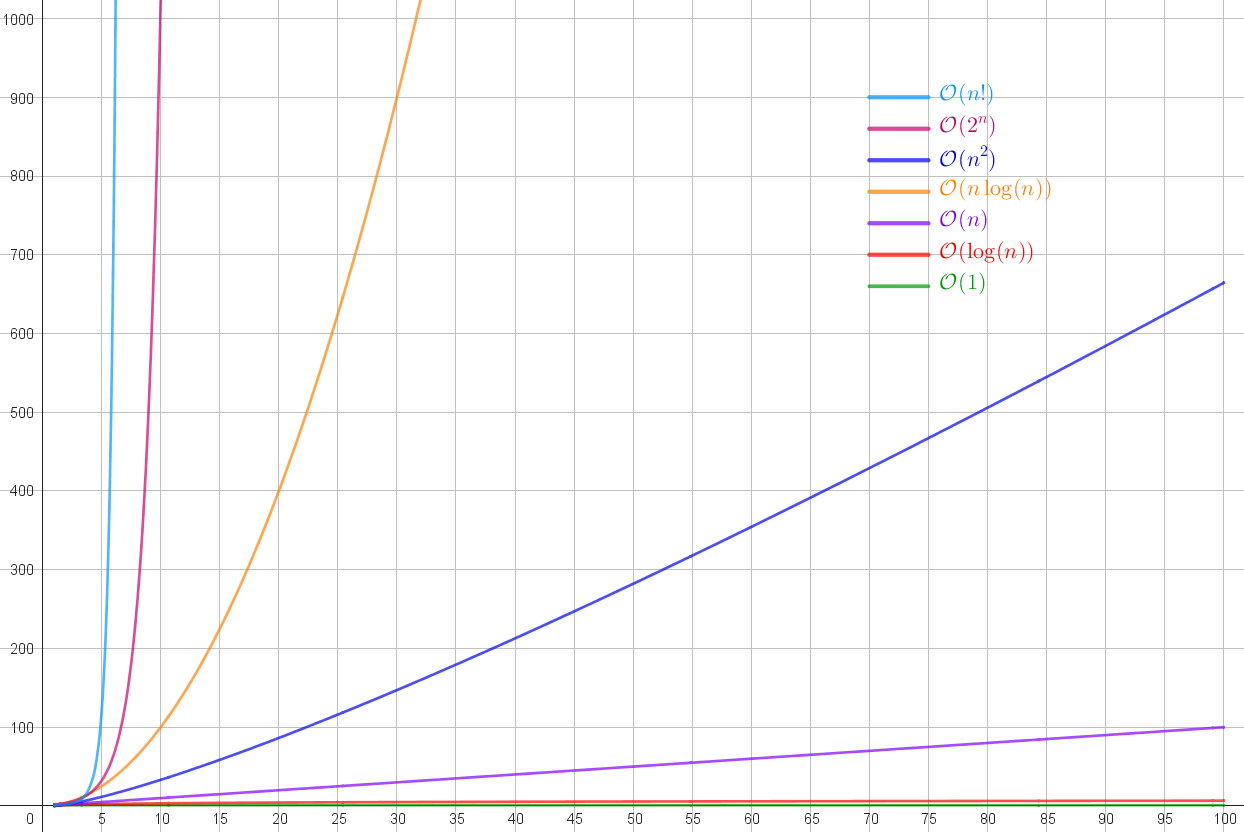
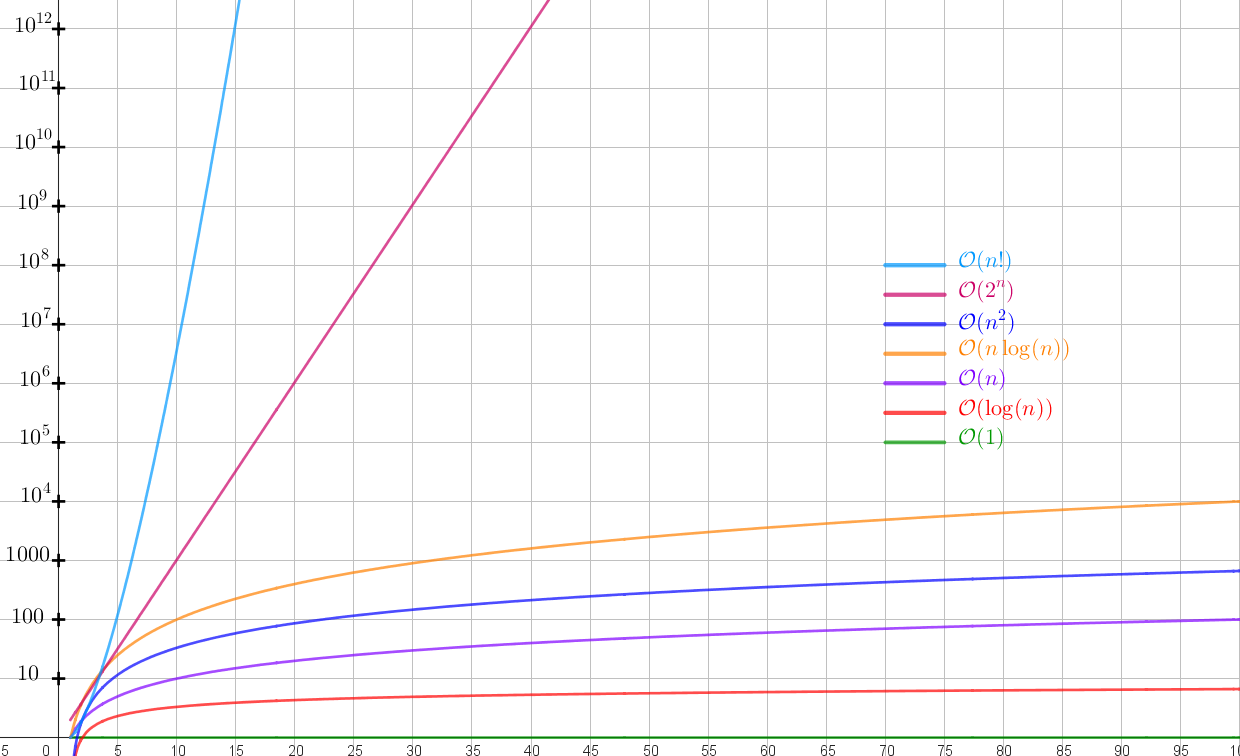
On peut mettre les ordonnées sur une échelle logarithmique pour mieux voir l'évolution des plus rapides.
Remarques
Multiplier la taille de données par \(10\) revient à multiplier le temps d’exécution au pire des cas :
- par un multiple de \(10\) si l’algorithme est de complexité linéaire ;
- par un multiple de \(10^2=100\) si l’algorithme est de complexité quadratique ;
- Si l’algorithme est de complexité logarithmique alors il faut ajouter un multiple de \(log(10)\) au temps d’exécution.
- Et si l’algorithme est de complexité exponentielle, alors il faut mettre le temps d’exécution à la puissance \(10\). Ce qui peut croître très vite...
Temps d'exécution
Le tableau ci-dessous donne le temps approximatif d’exécution en fonction de la taille des données. Nous supposerons qu’une instruction élémentaire prend 1 µs (\(10^{-6}\) secondes). Un temps astronomique est supérieur à un milliard de milliards d’années.
| Taille (\(n\)) | \(\log(n)\) | \(n\) | \(n\log(n)\) | \(n^2\) | \(2^n\) | \(n!\) |
|---|---|---|---|---|---|---|
| 10 | 3 µs | 10 µs | 30 µs | 100 µs | 1000 µs | 3 s |
| 100 | 7 µs | 100 µs | 700 µs | 1/100 s | \(10^{14}\) siècles | astronomique |
| 1000 | 10 µs | 1000 µs | 1/100 s | 1 s | astronomique | astronomique |
| 10000 | 13 µs | 1/100 s | 1/7 s | 1,7 min | astronomique | astronomique |
| 100000 | 17 µs | 1/10 s | 2 s | 2,8 h | astronomique | astronomique |
Ordre de grandeur
La complexité d’un algorithme ne prend en compte qu’un ordre de grandeur du nombre d’opérations (on néglige des choses). Pour représenter cette approximation on utilise une notation spécifique, la notation \(\mathcal{O}\) (qu'on lit "grand O"). La notation \(\mathcal{O}\) ne garde que l'expression avec lacroissance le plus rapide.
Par exemple, des algorithmes effectuant environ \(n\) opérations, \(2n+5\) opérations ou \(\frac{n}{2}\) opérations ont tous la même complexité : on la note \(\mathcal{O}(n)\) (lire « grand O de n »). De même, un algorithme en \((2n^2+3n+5)\) opérations aura une complexité de \(\mathcal{O}(n^2)\) : on néglige les termes \(3n\) et \(5\) qui sont de plus petits degrés que \(2n^2\) et donc croissent moins vite.
Par exemple, \(3n^2+5n−2=\mathcal{O}(n^2)\) a une complexité quadratique.
Exemples⚓︎
Exemple 1
def fonction1(n):
compteur = 0
for i in range(n):
print(f"Tour de boucle numéro {i}")
compteur = compteur + 1
print(compteur)
return compteur
Complexité
La fonction1 effectue \(1 + n \times (4)\) opérations, et même \(1 + n \times (6)\) si on prend en compte l'incrémentation et l'affectation de i, mais dans tous les cas, c'est une complexité linéaire : \(\mathcal{O}(n)\).
Exemple 2
def fonction2(n):
compteur = 0
for i in range(n):
print(f"Tour de boucle numéro {i}")
for j in range(n):
print(f"Tour de la boucle intérieure numéro {j}")
compteur = compteur + 1
print(compteur)
return compteur
Complexité
On a \(n\) fois \(n\) opérations, ou plus précisément \(n\) fois \(4n\) opérations. La fonction2 a une complexité quadratique : \(\mathcal{O}(n^2)\).
Exemple 3
def fonction3(n):
compteur = 0
for i in range(n):
print(f"Tour de boucle numéro {i}")
for j in range(i):
print(f"Tour de la boucle intérieure numéro {j}")
compteur = compteur + 1
print(compteur)
return compteur
Complexité
Dans la fonction3, la boucle for j in range(i) a une longueur qui dépend de i, donc quand \(i = 0\) elle ne s'applique pas, puis pour \(i = 1\) elle s'applique \(1\) fois, puis \(2\) fois, puis ... \(n-1\) fois.
Donc la fonction3 effectue \(1 + 2 + 3 + ... + (n-1)\) opérations.
On voit en cours de mathématiques (chapitre Suites arithmétiques) que ce calcul vaut : \(\dfrac{(n-1)\times n}{2} = \dfrac{n^2 - n}{2}\). C'est donc une complexité quadratique : \(\mathcal{O}(n^2)\).