21 Cours Tris

Ordre total⚓︎

Pour que la notion de tri ait un sens, il faut que les objets étudiés soient munis d'un ordre total.

C’est à dire que deux éléments sont toujours comparables grâce à une relation d’ordre. Parmi les types en python munis d’un ordre total on peut citer :

les entiers ;
les flottants ;
les chaînes de caractères.

Exemples⚓︎

Voici une liste d’entier [42, 3, 5, 9, 21, 9, 14] qui une fois triée sera [3, 5, 9, 9, 14, 21, 42]. C’est la relation d’ordre \(\leq\) qui est utilisée.
Pour deux caractères, l'ordre est celui de la table de caractères ASCII ou ISO.

🐍 Script Python

  >>> ord('a')
  97
  >>> ord('A')
  65
  >>> 'a' < 'A'
  False
  >>> 'A' < 'a'
  True
  >>> 'B' < 'a'
  True
  >>> 'Z' < 'a'
  True

Dans le cas d’une chaine de caractères, c’est la relation d’ordre lexicographique. Dans le cas de la liste : M = ["salut", "tout", "le", "monde"] la liste triée sera [’le’, ’monde’, ’salut’, ’tout’]. Attention car la comparaison des chaînes de caractères peut être biaisée par la casse (Majuscule / minuscules).

🐍 Script Python

  >>> 'abc' < 'bac'
  True
  >>> 'bon' < 'bonjour'
  True
  >>> 'Bonjour' < 'bonjour'
  True

Remarque⚓︎

On fera rarement des tris sur des objets qui sont eux-mêmes complexes. Mais vous pouvez néanmoins noter que, en Python :

les listes possèdent un ordre total, en comparant un à un le 1er élément de chaque liste, puis le 2e, etc. Une liste plus courte est considérée comme ayant des éléments plus petits.

🐍 Script Python

  >>> [1, 2, 3] < [3, 1, 2]
  True
  >>> [1, 2] < [1, 2, 3]
  True
  >>> [] < [1, 2]
  True

les tuples fonctionnent comme les listes

🐍 Script Python

  >>> (1, 2, 3) < (3, 1, 2)
  True
  >>> (1, 2) < (1, 2, 3)
  True
  >>> () < (1, 2)
  True

les dictionnaires ne possèdent pas d'ordre, et ne peuvent donc pas être comparés de manière native. Vous pouvez inventer un ordre si vous le souhaitez, mais il faudra alors le définir et l'implémenter.

Généralités sur les tris⚓︎

Nous nous intéresserons donc au tri d’une liste d’objets munis d’un ordre total.

Un algorithme de tri en informatique, est un algorithme qui permet d’organiser une collection d’objets selon une relation d’ordre déterminée. Notre collection d’objets, dans ce chapitre, sera, par exemple, une liste de nombres entiers munis de l'ordre usuel « est inférieur ou égal à », ou une liste de chaînes de caractères munis de l'ordre lexicographique.

Ainsi, il s'agira par exemple de demander le tri de la liste suivante : N = ["Ah !", "Non !", "C’est", "un", "peu", "court", "jeune", "homme !"].

Et d'obtenir : [’Ah !’, ’C’est’, ’Non !’, ’court’, ’homme !’, ’jeune’, ’peu’, ’un’].

Tri en place⚓︎

Un tri est dit « en place » s’il est effectué directement dans la structure de donnée initiale, et ne nécessite pas l’allocation d’une nouvelle structure.

Tri stable⚓︎

Un tri est dit stable s’il préserve l’ordonnancement initial des éléments que l’ordre considère comme égaux.

Par exemple, imaginez que vous vouliez trier la collection de bouteilles ci-dessous par ordre de volume (le volume est indiqué sous la bouteille) :

Si vous obtenez ceci, alors votre tri n’était pas stable :

En effet, la bouteille noire de volume 1 se trouve maintenant avant la bouteille bleue de même volume alors qu’elle devrait être après. Il en est de même pour les deux bouteilles de volume 4 qui sont inversées par rapport à l’ordre initial. Avec un tri stable, on aurait obtenu :

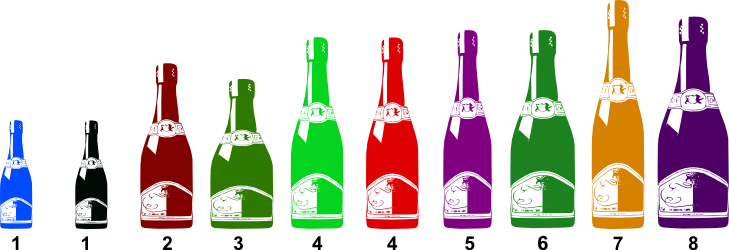
Tri par sélection⚓︎

Le principe du tri par sélection sur une liste d’entiers est le suivant :

on parcourt l’intégralité de la liste à la recherche du petit élément ;
une fois sélectionné ce plus petit élément, on le permute avec le tout premier élément de la liste (celui d’indice 0) ; le plus petit élément de la liste est alors en première position ;
on parcourt alors le reste de la liste pour sélectionner son plus petit élément, que l’on permute alors avec le deuxième élément de la liste (d’indice 1) ;
on recommence jusqu’à placer l’avant-dernier élément à sa place et la tâche est terminée.

Le tri par sélection se fait en place (on fait des échanges dans la liste de départ) et est non stable (en échangeant le plus petit élément avec le 1er élément, on peut placer cet élément derrière un autre qui lui est égal, et qui aurait donc dû rester derrière).

Exemple⚓︎

Voici une illustration du fonctionnement du tri par sélection sur un tableau de 6 éléments .

En vert ce qui est déjà trié, en rouge le nouvel élement, qui a été échangé avec le bleu.

12	9	3	7	14	11
3	9	12	7	14	11
3	7	12	9	14	11
3	7	9	12	14	11
3	7	9	11	14	12
3	7	9	11	12	14

Observer qu’une fois que l’avant-dernier élément est en place, le dernier l’est aussi.

À vous de faire la même chose sur le tableau suivant :

9	4	5	4	1	3

Solution

9	4	5	4	1	3
1	4	5	4	9	3
1	3	5	4	9	4
1	3	4	5	9	4
1	3	4	4	9	5
1	3	4	4	5	9

Tri par insertion⚓︎

Le principe du tri par insertion est d’insérer l’élément en cours (d’indice i) à sa place parmi les éléments triés qui le précède.

La plupart des personnes l’utilisent naturellement pour trier des cartes à jouer. Imaginez un paquet de carte sur une table, et dans votre main, des cartes déjà triées. Vous saisissez une carte (l’élément d’indice i) et vous la rangez dans votre main à la bonne place (on trie cet élément parmi les éléments triés qui le précède). Puis on recommence...

En général, le tri par insertion est beaucoup plus lent que d’autres algorithmes comme le tri rapide (ou quicksort) et le tri fusion pour traiter de grandes séquences, car sa complexité pour de grandes données est quadratique. Le tri par insertion est cependant considéré comme le tri le plus efficace sur des entrées de petite taille. Il est aussi très rapide lorsque les données sont déjà presque triées. Pour ces raisons, il est utilisé en pratique en combinaison avec d’autres méthodes comme le tri rapide.

Le tri par insertion est un tri stable (conservant l’ordre d’apparition des éléments égaux) et un tri en place (il n’utilise pas de liste auxiliaire).

Exemple⚓︎

Voici une illustration du fonctionnement du tri par insertion sur un tableau de 6 éléments :

En vert ce qui est déjà trié, en rouge le nouvel élement inséré.

12	9	3	7	14	11
9	12	3	7	14	11
3	9	12	7	14	11
3	7	9	12	14	11
3	7	9	12	14	11
3	7	9	3	11	14

À vous de faire la même chose sur le tableau suivant :

9	4	5	4	1	3

Solution

9	4	5	4	1	3
9	4	5	4	1	3
4	9	5	4	1	3
4	5	9	4	1	3
4	4	5	9	1	3
1	4	4	5	9	3
1	3	4	4	5	9

Autres tris⚓︎

Les deux algorithmes expliqués plus haut sont explicitement au programme de Première NSI et doivent être compris et maîtrisés. Mais il existe de nombreux autres algorithmes de tri, dont les plus connus sont probablement :

le tri à bulles (bubble sort), qui consiste à passer en revue tous les couples d'éléments, et à les échanger s'ils sont inversés, puis à recommencer jusqu'à ce qu'il n'y ait plus d'échange à faire
le tri fusion (merge sort) qui consiste à couper le tableau en deux sous-tableaux, à trier les sous-tableaux, puis à les fusionner. Pour trier les sous-tableaux, on peut de nouveau appliquer le tri fusion (donc re-diviser), ou utiliser un autre tri si l'on veut.
le tri rapide (quick sort) basé aussi sur du "diviser pour régner" : on choisit un pivot, on place à gauche les éléments plus petits que le pivot, et à droite les éléments plus grands. Le pivot est donc bien à sa place. Puis on trie chacun des deux sous-tableaux, par la méthode que l'on veut, mais a prioi le même tri rapide en choisissant un nouveau pivot.