23bis Exos Algorithmes gloutons

Reprise de l'Exercice 3 de la fiche précédente

Le problème du rendu de monnaie

Ce problème est un grand classique de l'algorithmique. Lorsque vous passez à la caisse d'un magasin quelconque, il n'est pas rare que le caissier doive vous rendre de l'argent car le montant que vous lui avez donné est supérieur à celui que vous devez payer.

Exemple. Supposons qu'on doive vous rendre la somme de 2,63€. Il y a plusieurs façons de procéder. On peut par exemple vous rendre 263 pièces de 1 centime, 125 pièces de 2 centimes et 13 pièces de 1 centime ou encore 5 pièces de 50 centimes, une de 10 centimes, une de 2 centimes et une de 1 centime.
Il y a bien évidemment énormément de possibilités pour vous rendre la dite somme. Mais il y a fort à parier que les solutions du type « 263 pièces de 1 cent » ne vous conviennent pas... Le problème qui se pose est donc de minimiser le nombre de pièces rendues pour un montant fixé.

La force brute consistera à énumérer toutes les combinaisons possibles pour rendre la monnaie, et à sélectionner celle qui minimise le nombre de pièces. Mais elle n'est (absolument) pas efficace.

La méthode gloutonne vise à optimiser la résolution d'un problème en partant du principe suivant : des choix locaux optimaux, étape après étape, devraient produire un résultat global optimal. Dans notre cas, on va répéter le choix de la pièce de plus grande valeur qui ne dépasse pas la somme restante.

Reprenons notre exemple. On doit donc rendre la somme de 2,63€ et on dispose du système de monnaie européen, à savoir les pièces de : 1, 2, 5, 10, 20, 50 centimes et 1 et 2 euros. La méthode gloutonne va d’abord choisir de rendre une pièce de 2 euros, il reste donc 63 centimes. Puis on choisira une pièce de 50 centimes etc. jusqu’à ce qu’il ne reste plus rien à rendre.

Le travail à faire : On donne le système monétaire suivant [200, 100, 50, 20, 10, 5, 2, 1] où chacun des nombres de la liste est une pièce exprimée en centimes d’euros.
Ecrire la fonction renduMonnaie prenant en argument le montant à rendre, et retournant la liste des pièces à rendre.

Testez votre fonction pour rendre la monnaie de \(6,78\) euros de façon optimale, c’est-à-dire avec le nombre minimal de pièces ?

Pour aller plus loin : On change de système monétaire, on a maintenant uniquement des pièces de \(1\), \(3\) et \(4\) centimes. Mettez à jour votre programme et faites des tests. Qu'en pensez-vous ?

Le problème du choix d'activités (pour ceux qui ont fini le reste)

On considère un ensemble d’activités, chacune possédant une date de début et une date de fin. Pour des raisons logistiques, on ne peut pas programmer des activités se déroulant en même temps. La question est la suivante :
quel est le nombre maximal d’activités que l’on va pouvoir planifier ?

Formalisons tout d'abord ce problème avec quelques notations mathématiques :

• L'ensemble des \(n\) activités peut être modélisé par un n-uplet de couples \(S = ((b1, e1), (b2, e2), ⋯ (bn, en))\) où \(bi\)représente la date de début de l'activité \(i\) et \(ei\) sa date de fin.
• On suppose que pour tout \(i\) entre \(1\) et \(n\), \(bi < ei\) et que l'activité \(i\) se déroule pendant l'intervalle \([bi ; ei[\)
• Deux activités \(i\) et \(j\) sont dites compatibles si \(bi ≥ ej\) ou \(bj ≥ ei\). On peut dans ce cas les programmer toutes les deux.
  

Notre question peut alors être reformulée comme suit : on cherche un sous-ensemble d’activités compatibles dont le cardinal (l'effectif) est le plus grand possible.

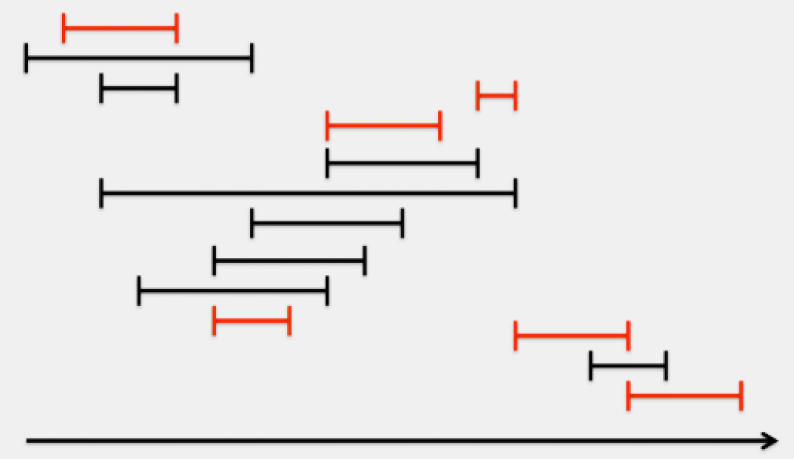
Exemple : Considérons l'ensemble d'activités \(S\) :
\(S = ((1,4), (0,6), (3,5), (12,13), (8,11), (8,12), (2,13), (6,10), (5,9), (3,8), (5,7), (13,16), (15,17), (16,19))\)

Il est relativement facile de voir visuellement que le nombre maximal d'activités que l'on peut planifier est \(6\), et que celles-ci sont celles marquées en rouge dans le schéma suivant :

Travail à faire : Ecrire une fonction choixActivites qui prend en argument la liste de toutes les activités S et retourne la liste des activités choisies C.

L'approche "force brute" n'étant pas vraiment envisageable, vous devrez imaginer une approche gloutonne, en triant les activités au préalable (par durée totale, par date de début, par date de fin, etc).