09 Exos Fonctions Compléments Correction

Exercice 1⚓︎

Écrire une fonction table avec un argument n qui produit l’affichage de la table de n (de $n\times 1$ à $n\times 10$) lorsqu'on l’appelle. Tester l’instruction table(2) dans le Shell.
🐍 Script Python
```
def table(n):
    for nombre in range(1, 11):
        print(f"{nombre:2} * {n} = {nombre * n}")
```
Modifier la fonction précédente de la manière suivante :
elle prend maintenant 3 paramètres : n, debut, fin
elle va afficher la table de n de $n\times $début à $n\times $fin
par défaut, debut vaut 1 et fin vaut 10, mais on peut décider de les modifier lors de l'appel de la fonction.
Ainsi, table(9) va afficher la table de 9 entre $9\times 1$ et $9\times 10$ ;
mais table(9, 0, 12) va afficher la table de 9 entre $9\times 0$ et $9\times 12$ ;
🐍 Script Python
```
def table(n, debut=1, fin=10):
    for nombre in range(debut, fin + 1):
        print(f"{nombre:2} * {n} = {nombre * n}")
```
Comment appeler la fonction pour faire afficher la table de 7 entre $7\times 1$ et $7\times 12$ ?
🐍 Script Python
```
table(7, 1, 12)
```
ou
🐍 Script Python
```
table(n=7, fin=12)
```

Exercice 2⚓︎

Écrire une fonction (ou procédure) repete qui répète le mot ’NSI’ un certain nombre de fois au choix, passé en paramètre.
🐍 Script Python
```
def repete(n):
    print(n * 'NSI')
```
Appel de la fonction :
🐍 Script Python
```
repete(5)
### NSINSINSINSINSI
```
Par défaut, le texte sera répété 2 fois.

Exercice 3⚓︎

Écrire une fonction qui prend en paramètres deux nombres x et y et renvoie le résultat de x² + y².

🐍 Script Python

def dist_carree(x, y):
  return x ** 2 + y ** 2

print(f"dist_carree(3, 4) = {dist_carree(3, 4)}")
### dist_carree(3, 4) = 25

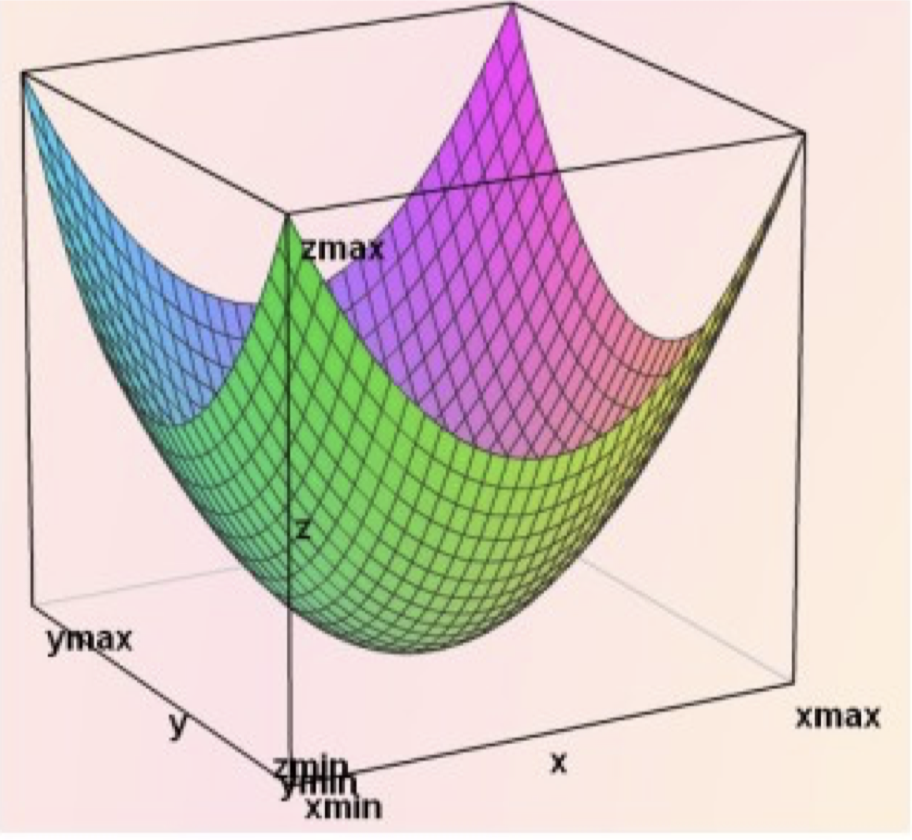
Pour information, la représentation graphique de cette fonction de deux variables dans un repère orthonormé de l’espace (paraboloïde) :

Exercice 4⚓︎

Écrire une fonction perimetre_triangle() qui prend en paramètres les 3 longueurs des côtés d’un triangle (en cm) et qui retourne son périmètre.
🐍 Script Python
```
def perimetre_triangle(a, b, c):
    p = a + b + c
    return p
```

Écrire une fonction est_constructible qui renvoie s’il est possible de construire un triangle avec trois segments de mesures données. Cette fonction devra renvoyer un booléen.

🐍 Script Python

def est_constructible(a, b, c):
    if a > b + c or b > a + c or c > a + b:
        return False
    else:
        return True

Cette fonction retourne un booléen que l'on peut utiliser directement dans un test :

🐍 Script Python

a = 5
b = 6
c = 2
if est_constructible(a, b, c):
    print(f"Le triangle de côtés de longueurs {a}, {b}, {c} est constructible.")
else:
    print(f"Le triangle de côtés de longueurs {a}, {b}, {c} n'est pas constructible.")
### Le triangle de côtés de longueurs 5, 6, 2 est constructible.
a = 12
b = 4
c = 3
if est_constructible(a, b, c):
    print(f"Le triangle de côtés de longueurs {a}, {b}, {c} est constructible.")
else:
    print(f"Le triangle de côtés de longueurs {a}, {b}, {c} n'est pas constructible.")
### Le triangle de côtés de longueurs 12, 4, 3 n'est pas constructible.

Utiliser la fonction input et les deux fonctions précédentes pour écrire une fonction saisie_puis_perimetre qui demande à l'utilisateur la longueur de chaque côté d’un triangle (en cm) et, si celui-ci est bien constructible, retourne son périmètre.

🐍 Script Python

def saisie_puis_perimetre():
    a = float(input("Premier côté ? "))
    b = float(input("Deuxième côté ? "))
    c = float(input("Troisième côté ? "))
    if est_constructible(a, b, c):
        return perimetre_triangle(a, b, c)

Exercice 5⚓︎

Voici une fonction qui affiche à l'écran les paroles de la chanson "Babar" : https://comptines.tv/babar

🐍 Script Python

def paroles_Babar():
    print("""Babar dans la forêt
Partit se promener
Babar a rencontré
Un oiseau bleu qui faisait
Cui,Cui,Cui,Cui,Cui,Cui,
Cui,Cui,Cui,Cui,Cui,Cui,

Babar dans la forêt
Partit se promener
Babar a rencontré
Un canard gris qui faisait
Coin,Coin,Coin,Coin,Coin,Coin,
Coin,Coin,Coin,Coin,Coin,Coin,

Babar dans la forêt
Partit se promener
Babar a rencontré
Un corbeau noir qui faisait
Croa,Croa,Croa,Croa,Croa,Croa,
Croa,Croa,Croa,Croa,Croa,Croa,

Babar dans la forêt
Partit se promener
Babar a rencontré
Un grillon vert qui faisait
Cri,Cri,Cri,Cri,Cri,Cri,
Cri,Cri,Cri,Cri,Cri,Cri,
""")

paroles_Babar()

Solution :

Factoriser le code dans une fonction couplet, avec des paramètres bien choisis, de manière à ne pas répéter le code commun à tous les couplets. La chanson donnée a des couplets qui n'ont que peu de variations entre eux :

l'animal rencontré
le cri de cet animal

On peut donc factoriser tout le texte à afficher, en utilisant des variables pour l'animal et pour le cri.

🐍 Script Python

def couplet(animal, cri):
    print("""Babar dans la forêt
Partit se promener
Babar a rencontré
Un """ + animal 
+" qui faisait\n"
+ 5 * (cri+",") + "\n" 
+ 5 * (cri+","))

def paroles_Babar_factorise():
    couplet("oiseau bleu", "Cui")
    print()
    couplet("canard gris", "Coin")
    print()
    couplet("coirbeau noir", "Croa")
    print()
    couplet("grillon vert", "Cri")

paroles_Babar_factorise()

Exercice 6⚓︎

Factoriser le code suivant :

🐍 Script Python

from turtle import *
up()
goto(-300, 0)
#première maison
down()
forward(90)
left(90)
forward(60)
left(30)
forward(30)
left(120)
forward(30)
right(60)
forward(60)
left(90)
forward(60)
left(90)
up()
forward(120)
#deuxième maison
down()
forward(150)
left(90)
forward(100)
left(30)
forward(50)
left(120)
forward(50)
right(60)
forward(100)
left(90)
forward(100)
left(90)
up()
forward(200)
#troisième maison
down()
forward(210)
left(90)
forward(140)
left(30)
forward(70)
left(120)
forward(70)
right(60)
forward(140)
left(90)
forward(140)
left(90)
up()
forward(280)

done() ## pour la version sur Capytale
a = input() ## sur un autre éditeur, on peut aussi mettre un imput() pour éviter que la fenêtre ne se ferme...

Solution :

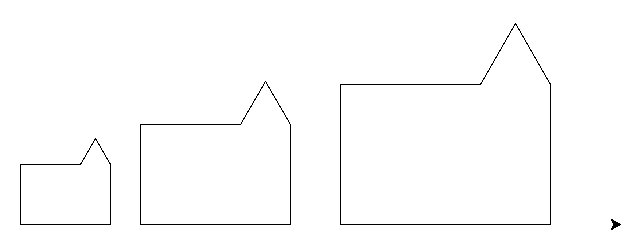
Le code donné dessine l'image suivante :

🐍 Script Python

from turtle import *

# on définit une fonction qui dessine une maison avec un paramètre pour la taille
# et on exprime toutes les longueurs en fonction de ce paramètre
def maison(taille):
    down()
    forward(3 * taille)
    left(90)
    forward(2 * taille)
    left(30)
    forward(taille)
    left(120)
    forward(taille)
    right(60)
    forward(2 * taille)
    left(90)
    forward(2 * taille)
    left(90)
    up()
    forward(4 * taille)

up()
goto(-200, 0)
# pour l'appel, on peut alors appeler 3 fois la fonction avec la taille appropriée :
#première maison
maison(30)
#deuxième maison
maison(50)
#troisième maison
maison(70)

# Ou alors on parvient à écrire une boucle et à exprimer la taille :
for i in range(3):
    maison(30 + i * 20)

Exercice 7⚓︎

L'anniversaire de Théo tombe le 29 février. Il a rédigé un programme qui affiche s'il aura un 29 février cette année ou non.

Il l'a codé de la manière suivante :

🐍 Script Python

def annee_chouette(a):
    if a%400 == 0 or (a%4 == 0 and a%100 != 0) :
        print("Chouette, cette année, j'ai un anniversaire !")
    else:
        print("Tant pis, encore pas cette année...")

Conformément aux "bonnes pratiques", créez une fonction bien nommée pour calculer le booléen correspondant au test du if.

Solution :

L'anniversaire de Théo tombe le 29 février. Il a rédigé un programme qui affiche s'il aura un 29 février cette année ou non.

Il l'a codé de la manière suivante :

🐍 Script Python

def annee_chouette(a):
    if a%400 == 0 or (a%4 == 0 and a%100 != 0) :
        print("Chouette, cette année, j'ai un anniversaire !")
    else:
        print("Tant pis, encore pas cette année...")

Conformément aux "bonnes pratiques", créez une fonction bien nommée pour calculer le booléen correspondant au test du if.

L'idée est que la fonction annee_chouette(a) appelle, dans la condition du if, une fonction qui renvoie un booléen. Comme il s'agit de tester si l'année est bissextile ou non, c'est ainsi qu'on va l'appeler :

🐍 Script Python

def annee_chouette(a):
    if est_bissextile(a):
        print("Chouette, cette année, j'ai un anniversaire !")
    else:
        print("Tant pis, encore pas cette année...")

Reste à définir cette fonction est_bissextile(a) :
soit on utilise directement la formule booléenne qui était donnée :

🐍 Script Python

def est_bissextile(a):
    return a%400 == 0 or (a%4 == 0 and a%100 != 0)

Soit, de manière plus détaillée, mais en fait un peu plus lisible, on peut régler les cas les uns après les autres, en profitant de la sortie de fonction par le return pour ne pas utiliser de else :

🐍 Script Python

def est_bissextile_autre(a):
    if a%4 != 0:
        return False
    if a%400 == 0:
        return True
    if a%100 == 0:
        return False
    return True

Ici, dans la majorité des cas (année non bissextile), un seul test booléen sera calculé...

Exercice 8⚓︎

Le programme suivant est tout a fait optimisé, sans répétition dans l'écriture.

🐍 Script Python

from turtle import *

def figure1():
    for i in range(6):
        down()
        for j in range(10):
            for k in range(6):
                forward(50)
                left(60)
            left(36)
        up()
        left(60)
        forward(120)

up()
goto(0, -100)
speed(10)
down()
figure1()
done() ## pour Capytale

Mais, d'une part, il contient des boucles dans des boucles, et d'autre part, il apparaît nettement qu'il est composé de petites parties auxquelles il est aisé de donner du sens (qui dessinent une figure plutôt simple).

Séparer ce code avec des plus petites fonctions bien nommées qui pourront être appelées dans la fonction figure1().

Solution :

Le programme donné dessine la figure suivante :

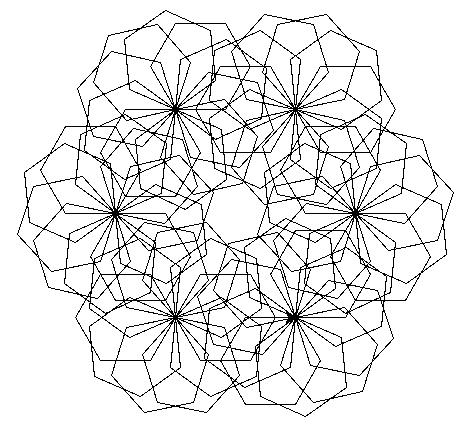
On constate qu'elle est constituée de 6 rosaces, chacune constituée de 10 hexagones.
On peut donc définir :

une fonction hexagone() qui contiendra la boucle for la plus intérieure ;
une fonction rosace10hexagones() (ou un autre nom explicite) qui contient la boucle for intermédiaire ;
une fonction figure1() qui ne contiendra qu'une seule boucle for, et fera appel à la fonction rosace10hexagones().

🐍 Script Python

from turtle import *

def hexagone():
    for i in range(6):
        forward(50)
        left(60)

def rosace10hexagones():
    for i in range(10):
        hexagone()
        left(36)

def figure1():
    for i in range(6):
        down()
        rosace10hexagones()
        up()
        left(60)
        forward(120)

figure1()

On peut également rendre chacune de ces fonctions plus configurables, en passant des arguments en paramètres, par exemple la longueur du côté pour la fonction hexagone(cote), ou le nombre d'hexagones utilisés pour la fonction rosace(n)...
Ce serait très très bien. Mais ce n'était pas l'objet de cet exercice.
Ce qui est l'objet de cet exercice, en revanche, et auquel il faut apporter une attention particulière, c'est de bien nommer les fonctions (et les variables) pour qu'on comprenne immédiatement ce qu'elles sont censées faire.

Exercice 9 - pour les plus rapides⚓︎

Ecrire une fonction qui prend en paramètres les 3 longueurs des côtés d’un triangle (en cm) et renvoie son aire en sortie.

Indication. Faire une recherche internet sur la formule de Héron.

📋 Texte

On testera le programme à l&rsquo;aide d&rsquo;un triangle rectangle (dimensions de votre choix) dont l&rsquo;aire est facile à calculer.

🐍 Script Python

from math import sqrt

def aire_triangle_heron(a, b, c):
    if not(est_constructible(a, b, c)):     #on peut réutiliser la fonction de l'exo 1 pour faire cette vérification
        print("Triangle non constructible")
        return -1
    p = (a + b + c) / 2
    S = sqrt(p * (p - a) * (p - b) * (p - c))
    return S

Tests divers :

🐍 Script Python

print(f"aire_triangle_heron(4, 5, 3) : {aire_triangle_heron(4, 5, 3)}")
### aire_triangle_heron(4, 5, 3) : 6.0
print(f"aire_triangle_heron(4, 5, 6) : {aire_triangle_heron(4, 5, 6)}")
### aire_triangle_heron(4, 5, 6) : 9.921567416492215
print(f"aire_triangle_heron(1, 5, 6) : {aire_triangle_heron(1, 5, 6)}")
### aire_triangle_heron(1, 5, 6) : 0.0
print(f"aire_triangle_heron(1, 5, 7) : {aire_triangle_heron(1, 5, 7)}")
### Triangle non constructible
### aire_triangle_heron(1, 5, 7) : -1
print(f"aire_triangle_heron(10000000000, 10000000000, 0.000000001) : {aire_triangle_heron(10000000000, 10000000000, 0.000000001)}")
### aire_triangle_heron(10000000000, 10000000000, 0.000000001) : 0.0

(Source Wikipédia) La formule de Héron présente une instabilité lors du calcul numérique, qui se manifeste pour les triangles en épingle, c’est-à-dire dont un côté est de dimension très petite par rapport aux autres (confrontation de petites et grandes valeurs).

a. Tester avec des valeurs extrêmes (exemple : $a = b = 1000000000$ et $c = 0,000000001$). Tests divers :

🐍 Script Python

print(f"aire_triangle_heron(10000000000, 10000000000, 0.000000001) : {aire_triangle_heron(10000000000, 10000000000, 0.000000001)}")
### aire_triangle_heron(10000000000, 10000000000, 0.000000001) : 0.0

-> L'aire d'un tel triangle ne devrait pas être nulle !!!

D'où vient le problème ?

Les entiers sont codés sur un nombre de bits qui dépend de leur taille. Les opérations sont exactes. On peut tester le calcul :

🐍 Script Python

123456789123456789 + 1 - 123456789123456789

On obtient 1, comme attendu.

En revanche, les flottants sont codés sur un nombre fixe de bits, de manière à coder leur ordre de grandeur (puissance de $10$ correspondante, et un nombre fixe de chiffres significatifs. Lorsque le nombre comporte davantage de chiffres, les derniers sont perdus.
Lors d'opérations entre nombres flottants d'ordres de grandeur différents, cela peut vraiment poser problème.On peut tester le calcul :

🐍 Script Python

123456789123456789.0 + 1.0 - 123456789123456789.0

On obtient 0.0, ce qui est faux.

Il suffit de n'en garder que le début pour voir où est le problème :

🐍 Script Python

123456789123456789.0 + 1.0

On obtient 1.2345678912345678e+17, ce qui est une valeur arrondie, qui n'a pas gardé les unités.

b. En choisissant les noms de côtés de sorte à ce que $a > b > c$, et en réorganisant les termes de façon à optimiser les grandeurs ajoutées ou soustraites, on obtient la formule de Kahan, plus stable :

$A=\frac{1}{4}\sqrt{(a+(b+c))(c-(a-b))(c+(a-b))(a+(b-c))}.$

Editer une nouvelle fonction utilisant cette formule de Kahan, puis tester les deux fonctions avec des valeurs extrêmes (exemple : $a = b = 1000000000$ et $c = 0,000000001$).

🐍 Script Python

def aire_triangle_kahan(a, b, c):
  if not(constructible(a, b, c)):       # on fait la vérification de la constructibilité
    print("Triangle non constructible")
    return -1
  [a, b, c] = sorted([a, b, c])         # on peut remettre les valeurs dans l'ordre, au cas où elles ne le seraient pas
  A = sqrt((c + (b + a)) * (a - (c - b)) * (a + (c - b)) * (c + (b - a))) / 4
  return A

Tests divers :

🐍 Script Python

print(f"aire_triangle_kahan(4, 5, 3) : {aire_triangle_kahan(4, 5, 3)}")
### aire_triangle_kahan(4, 5, 3) : 6.0
print(f"aire_triangle_kahan(4, 5, 6) : {aire_triangle_kahan(4, 5, 6)}")
### aire_triangle_kahan(4, 5, 6) : 9.921567416492215
print(f"aire_triangle_kahan(1, 5, 6) : {aire_triangle_kahan(1, 5, 6)}")
### aire_triangle_kahan(1, 5, 6) : 0.0
print(f"aire_triangle_kahan(1, 5, 7) : {aire_triangle_kahan(1, 5, 7)}")
### Triangle non constructible
### aire_triangle_kahan(1, 5, 7) : -1
print(f"aire_triangle_kahan(10000000000, 10000000000, 0.000000001) : {aire_triangle_kahan(10000000000, 10000000000, 0.000000001)}")
### aire_triangle_kahan(10000000000, 10000000000, 0.000000001) : 5.0
print(f"aire_triangle_kahan(0.000000001, 10000000000, 10000000000) : {aire_triangle_kahan( 0.000000001, 10000000000, 10000000000)}")
### aire_triangle_kahan(0.000000001, 10000000000, 10000000000) : 5.0