02 Cours La représentation des entiers (le binaire)⚓︎
Version distribuée du cours NSI 02
Introduction : le système décimal⚓︎
Le système décimal désigne un système de représentation des nombres en base \(10\). Cela signifie que l'on utilise \(10\) symboles (les chiffres de 0 à 9) pour écrire les nombres.
Ces dix chiffres permettent de représenter les quantités de zéro à neuf.
Pour représenter dix unités, on fera un paquet de dix (une dizaine). On n'a plus de nouveau symbole, on utilise le symbole "\(1\)", mais en \textbf{position} dizaine : \(10\).
Pour la suite, on additionne les dizaines et les unités :
\(11 =1 \text{ dizaine} + 1 \text{ unité}\),
\(12=1 \text{ dizaine} + 2 \text{ unités}\),
...
\(21=2 \text{ dizaines} + 1 \text{ unité}\),
...
\(99=9 \text{ dizaines} + 9 \text{ unités}\).
\(99\) est le plus grand nombre possible à deux chiffres.
Le nombre suivant, cent, représente un paquet de \(10 \times 10 = 100\) (une centaine).
\(100 = 10 \times 10 = 10^2\).
De \(100\) à \(999\), les nombres se représentent avec \(3\) chiffres.
Pour représenter le nombre suivant, on écrit : \(1000 = 10 \times 100 = 10^3\).
Et ainsi de suite.
Le système décimal utilise 10 chiffres, et leurs positions représentent les puissances de 10 successives.
C'est un système positionnel : le 2 de 523 n'a pas la même valeur que le 2 de 132.
4523 = 4 milliers + 5 centaines + 2 dizaines + 3 unités
4523 = (4 × 103) + (5 × 102) + (2 × 101) + (3 × 100).
Autres bases de numération⚓︎
On peut selon ce principe imaginer une infinité de systèmes numériques fondés sur des bases différentes. Le choix de faire des paquets de \(10\) est sans doute dû au fait que nous ayons \(10\) doigts. Mais certaines civilisations avaient choisi la base \(20\) ou la base \(60\).
D'ailleurs, aujourd'hui, la base \(60\) est toujours utilisée pour la mesure du temps : 1 heure = 60 min = 3600 s.
Concernant la base vingt, nous en avons les vestiges dans la lecture des nombres en français : quatre-vingts, quatre-vingt-dix... à une époque, on pouvait rencontrer vingt-et-dix (\(30\)), deux-vingt (\(40\)), trois-vingt (\(60\)) !
Et si on n'avait que quatre symboles ?⚓︎
Imaginons un système numérique avec quatre symboles (on peut imaginer ce qu'on veut) :
♠ ♥ ♦ ♣
a b c d
0 1 2 3
Écrire les nombres suivants avec le système à quatre symboles :
| zéro : | neuf : | dix-huit : |
|---|---|---|
| un : | dix : | dix-neuf : |
| deux : | onze : | vingt : |
| trois : | douze : | vingt-et-un : |
| quatre : | treize : | trente-deux : |
| cinq : | quatorze : | quarante-huit : |
| six : | quinze : | soixante-trois : |
| sept : | seize : | soixante-quatre : |
| huit : | dix-sept : | soixante-cinq : |
Solution
| zéro : a | neuf : cb | dix-huit : bac |
|---|---|---|
| un : b | dix : cc | dix-neuf : bad |
| deux : c | onze : cd | vingt : bba |
| trois : d | douze : da | vingt-et-un : bbb |
| quatre : ba | treize : db | trente-deux : caa |
| cinq : bb | quatorze : dc | quarante-huit : daa |
| six : bc | quinze : dd | soixante-trois : ddd |
| sept : bd | seize : baa | soixante-quatre : baaa |
| huit : ca | dix-sept : bab | soixante-cinq : baab |
Un système numérique en base 4 utilise 4 symboles (chiffres), et leurs positions représentent les puissances de 4 successives.
bacd = (1 × 43) + (0 × 42) + (2 × 41) + (3 × 40).
Les systèmes de numération en informatique⚓︎
L'informatique est basée sur du courant électrique, qui passe, ou ne passe pas. Les ordinateurs modernes utilisent des transistors, qui jouent le rôle de petits interrupteurs, qui laissent ou non passer le courant. À un instant donné, il n'y a que deux positions possibles : la tension est nulle, ou elle ne l'est pas.
Il a donc fallu construire le codage des informations, dans les ordinateurs, sur un système à 2 états.
Ces deux états pourront être interprétés comme \(0\) (tension nulle) et \(1\) (tension non nulle).
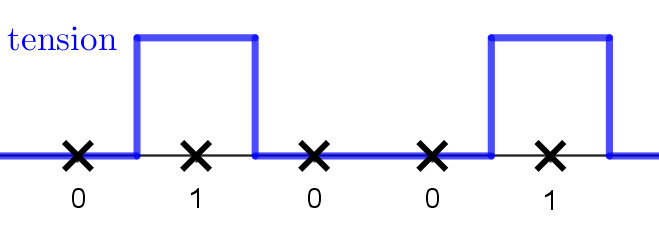
L'informatique utilise donc le système binaire (base 2), et tous les calculs vont se baser sur l'algèbre booléenne à 2 états (\(0\) et \(1\), False et True).
Deux symboles suffisent : on prend \(0\) et \(1\).
Et si on a deux symboles ? Le système binaire⚓︎
Écrire les nombres suivants avec le système binaire à deux symboles :
| zéro : | neuf : | dix-huit : |
|---|---|---|
| un : | dix : | dix-neuf : |
| deux : | onze : | vingt : |
| trois : | douze : | vingt-et-un : |
| quatre : | treize : | trente-deux : |
| cinq : | quatorze : | quarante-huit : |
| six : | quinze : | soixante-trois : |
| sept : | seize : | soixante-quatre : |
| huit : | dix-sept : | soixante-cinq : |
Solution
| zéro : \(0\) | neuf : \(1001\) | dix-huit : \(10010\) |
|---|---|---|
| un : \(1\) | dix : \(1010\) | dix-neuf : \(10011\) |
| deux : \(10\) | onze : \(1011\) | vingt : \(10100\) |
| trois : \(11\) | douze : \(1100\) | trente-et-un : \(11111\) |
| quatre : \(100\) | treize : \(1101\) | trente-deux : \(100000\) |
| cinq : \(101\) | quatorze : \(1110\) | quarante-huit : \(110000\) |
| six : \(110\) | quinze : \(1111\) | soixante-trois : \(111111\) |
| sept : \(111\) | seize : \(10000\) | soixante-quatre : \(1000000\) |
| huit : \(100\) | dix-sept : \(10001\) | soixante-cinq : \(1000001\) |
Un système numérique en base 2 utilise 2 symboles (chiffres), et leurs positions représentent les puissances de 2 successives.
101001 = (1 × 25) + (0 × 24) + (1 × 23) + (0 × 22) + (0 × 21) + (1 × 40).
101001 = 32 + 0 + 8 + 0 + 0 + 1.
Conversion décimal - binaire⚓︎
Convertissons 01001101 en décimal à l’aide du schéma ci-dessous :
| \(2^7\) | \(2^6\) | \(2^5\) | \(2^4\) | \(2^3\) | \(2^2\) | \(2^1\) | \(2^0\) |
|---|---|---|---|---|---|---|---|
| \(=128\) | \(=64\) | \(=32\) | \(=16\) | \(=8\) | \(=4\) | \(=2\) | \(=1\) |
| 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 |
Le nombre en base \(10\) est \(2^6 + 2^3 + 2^2 + 2^0 = 64 + 8 + 4 + 1 = 77\).
Allons maintenant dans l’autre sens et écrivons \(77\) en base 2. Il s’agit de faire une suite de divisions euclidiennes par 2. Le résultat sera la juxtaposition des restes. Le schéma ci-dessous explique la méthode mieux qu’un long discours :
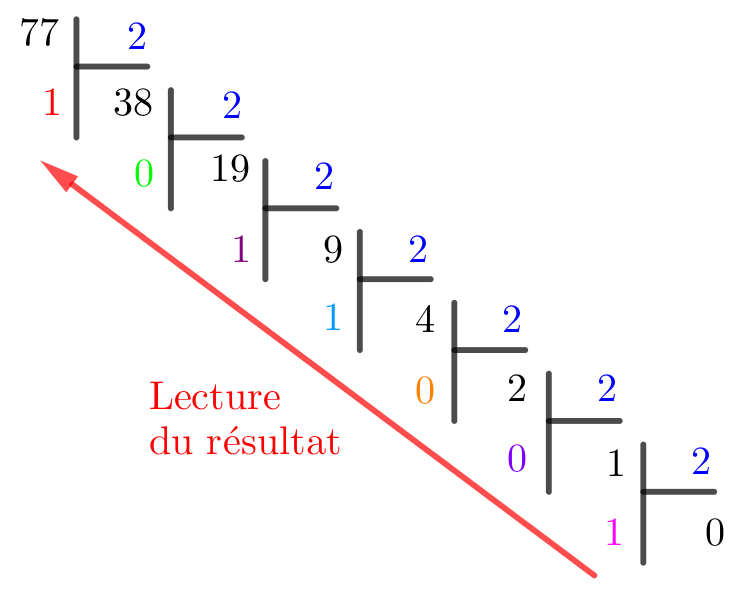
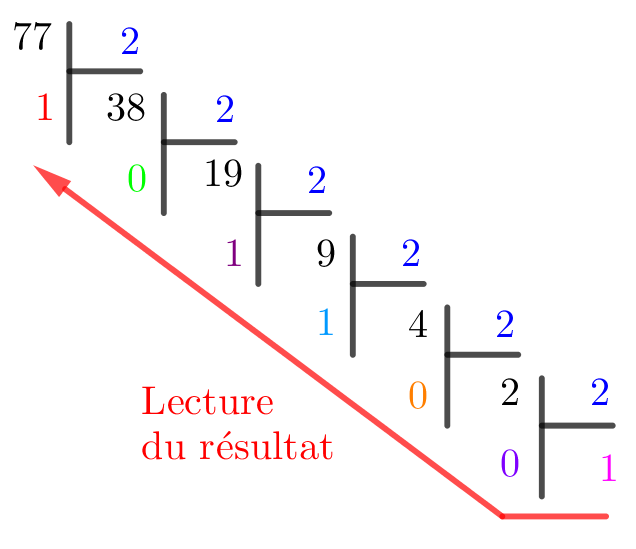
77 s’écrit donc en base 2 : 1001101. Si on l’écrit sur un octet, cela donne : 01001101.
Pourquoi ça marche ? (et pourquoi en prenant les restes dans l'ordre inverse ?)

Et si on a seize symboles ? Le système hexadécimal⚓︎
Un système hexadécimal demande plus de dix symboles pour écrire les 16 chiffres du système.
Nous prendrons sans surprise :
zéro : \(0\) ; un : \(1\) ; deux : \(2\) ; trois : \(3\) ; quatre : \(4\) ; cinq : \(5\) ; six : \(6\) ; sept : \(7\) ; huit : \(8\) ; neuf : \(9\) ;
auxquels nous ajouterons :
dix : \(a\) ; onze : \(b\) ; douze : \(c\) ; treize : \(d\) ; quatorze : \(e\) et quinze : \(f\).
Ainsi :
\(10\) signifie \(1\) paquet de seize
\(100\) signifie \(1\) paquet de seize \(\times\) seize \(= 256\)
Un système numérique en base 16 utilise 16 symboles, et leurs positions représentent les puissances de 16 successives.
2af = 2 paquets de 256 + dix paquets de 16 + quinze unités
2af = (2 × 162) + (10 × 161) + (15 × 160).
Le système hexadécimal n'est pas utilisé tel quel en informatique, mais il est bien plus concis que le binaire, tout en permettant une conversion vers le binaire (presque) sans calcul. On l'utilise donc parfois pour représenter des nombres qui sont en fait codés en binaire dans l'ordinateur : les valeurs numériques des couleurs, les adresses IPv6, etc.
Conversion hexadécimal - binaire⚓︎
Le tableau ci-dessous montre la représentation des nombres de 0 à 15 dans les bases 10, 2 et 16.
| Décimal | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Binaire | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
| Hexadécimal | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
Chaque "chiffre" en hexadécimal correspond à une puissance de \(16\). Comme \(16 = 2^4\), cela correspond en fait à un groupement de \(4\) chiffres en binaire.
Par exemple :
\(6\) en hexadécimal s'écrit \(0110\) en binaire
\(4\) en hexadécimal s'écrit \(0100\) en binaire
\(D\) en hexadécimal s'écrit \(1101\) en binaire (et \(13\) en décimal)
Chaque "chiffre" en hexadécimal correspond à une puissance de \(16\). Comme \(16 = 2^4\), cela correspond en fait à un groupement de \(4\) chiffres en binaire.
Par exemple : prenons le nombre en écriture binaire \(0110 0100 1101\)
| hexa | \(6\) | \(4\) | \(D\) |
|---|---|---|---|
| décimal | \(6 \times 16^2\) | \(4 \times 16^1\) | \(13\) |
| décimal | \(6 \times 2^8\) | \(4 \times 2^4\) | \(13\) |
| décimal | \((0 \times 2^3 + 1 \times 2^2 + 1 \times 2^1 + 0)\times 2^8\) | \((0 \times 2^3 + 1 \times 2^2 + 0 \times 2^1 + 0)\times 2^4\) | \(1 \times 2^3 + 1 \times 2^2 + 0 \times 2^1 + 1 \times 2^0\) |
| décimal | \(0 \times 2^{11} + 1 \times 2^{10} + 1 \times 2^9 + 0 \times 2^8\) | \(0 \times 2^7 + 1 \times 2^6 + 0 \times 2^5 + 0 \times 2^4\) | \(1 \times 2^3 + 1 \times 2^2 + 0 \times 2^1 + 1 \times 2^0\) |
| binaire | \(0110\) | \(0100\) | \(1101\) |
Pour convertir de binaire à hexadécimal, ou de hexadécimal à binaire, il suffit donc de connaître l'écriture binaire des nombres de 0 à 15 (de 0 à F, écrits en hexadécimal). Aucun calcul n'est nécessaire.
- Pour convertir de binaire à hexadécimal, il suffit donc de faire des groupes de quatre bits (en commençant depuis la droite) et de convertir chaque nombre de 4 digits en hexadécimal.
- Pour convertir d'hexadécimal à binaire, il suffit de convertir chaque chiffre hexadécimal en son écriture binaire, et de les juxtaposer dans l'ordre.
Exercice 1⚓︎
Donnez la méthode pour passer de la base décimale à la base hexadécimale (dans les deux sens).
Solution
Il faut déjà savoir convertir les 15 symboles hexadécimaux en nombre décimal et inversement (voir le tableau).
De la base hexadécimale à la base décimale :
On mutliplie le chiffre des unités (le plus à droite) par 1,
le suivant par \(16\),
le suivant par \(16^2\)
et ainsi de suite.
La somme de tous ces produits donne la représentation décimale du nombre.
Exemple :
Sachant que \(E_{16} = 14_{10}\) et \(D_{16} = 13_{10}\),
\(5D3E_{16}\) vaut, en écriture décimale :
\(14 \times 1 + 3 \times 16^1 + 13 \times 16^2 + 5 \times 16^3 = 14 \times 1 + 3 \times 16 + 13 \times 256 + 5 \times 4096 = 23870\)
De la base décimale à la base hexadécimale :
On calcule le quotient et le reste de la division euclidienne du nombre par \(16\).
On divise de nouveau le quotient, et ainsi de suite jusqu'à ce que le quotient soit nul.
Les restes successifs, rangés du dernier au premier, représentent l'écriture hexadécimale.
Exemple :
\(23870 = 1491 \times 16 + 14\)
\(1491 = 93 \times 16 + 3\)
\(93 = 5 \times 16 + 13\)
\(5 = 0 \times 16 + 5\)
On récupère les restes : \(5\), \(13\), \(3\), et \(14\). L'écriture hexadécimale est : \(5D3E\).
Notation⚓︎
A partir de maintenant, dès que l'on utilise plusieurs bases, et qu'il faut donc préciser, pour chaque nombre, dans quelle base il est exprimé, on l'indiquera en indice :
\({1101}_{2}\) en binaire, \({13}_{10}\) en décimal, \({D}_{16}\) en hexadécimal. On peut écrire \({1101}_{2} = {13}_{10} = {D}_{16}\).
Les opérations⚓︎
On sait que, en binaire : \(0+0 = 0\) ; \(0+1 = 1\) ;
\(1+1 = 10\) c'est-à-dire \(1+1 = 0\) et on a une retenue de \(1\).
Les opérations fonctionnent sur la même méthode qu'en décimal, en tenant compte des retenues...
Commençons par nous rappeler comment on pose les opérations en décimal...
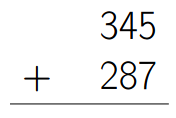
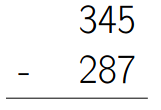
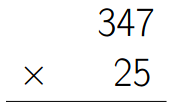
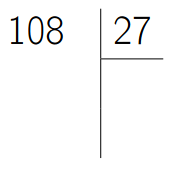
Et maintenant, en binaire, faire les opérations suivantes :


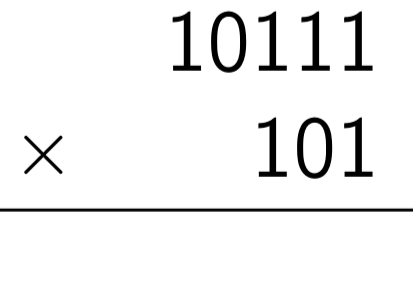
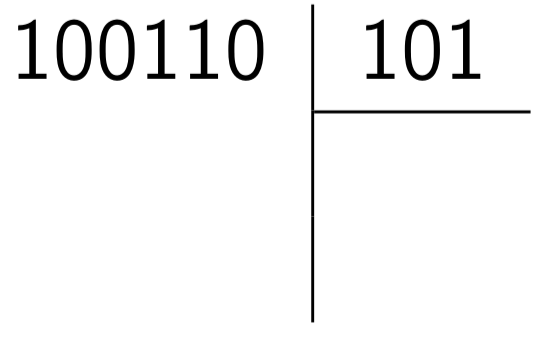
Solution


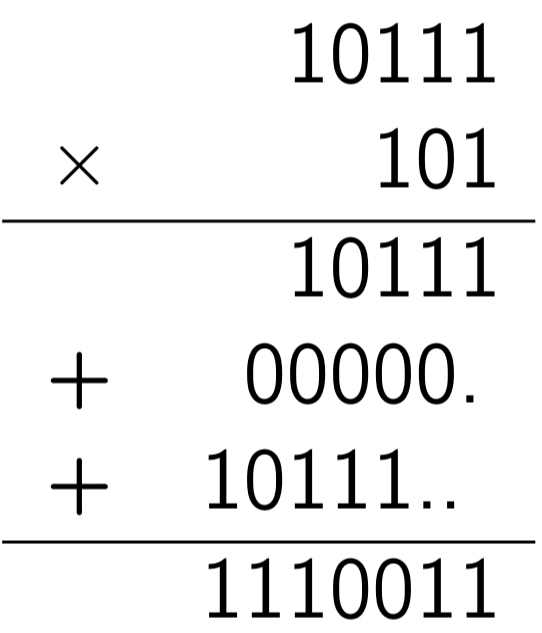

Et en bonus...⚓︎

